помогите найти периметр треугольника

Ответы
Ответ:
ед.;
ед,
Объяснение:
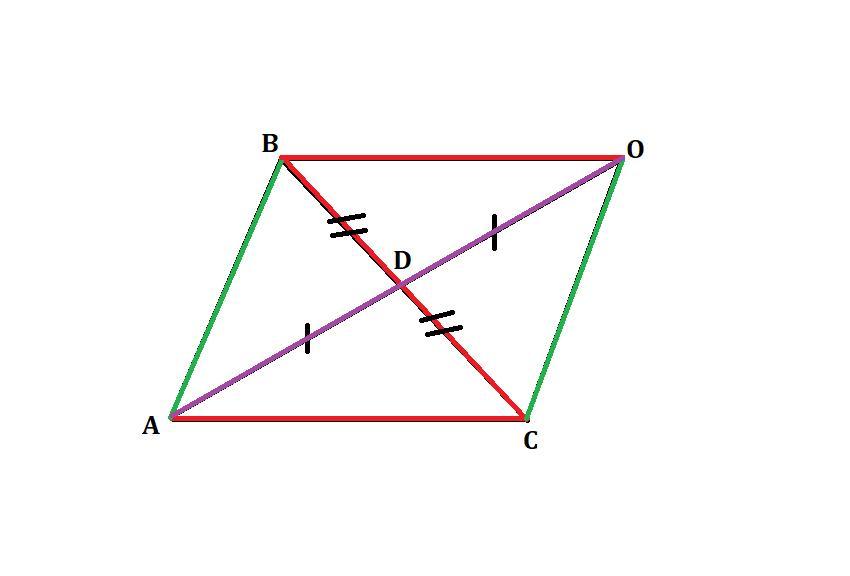
Условие данной задачи неполное, а из рисунка напрашивается вывод, что задача на тему "равнобедренные" треугольники ().
=========================================================
Пусть - равнобедренный.
Тогда ед.
Т.к. - медиана
ед.
Продлим медиану так, что
- середина отрезка
.
Также соединим точки ,
и
,
.
Получился четырёхугольник .
Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник - параллелограмм.
и
- диагонали параллелограмма
и они пересекаются.
Точка - пересечение диагоналей
и
.
Также в :
;
:
, то есть точкой пересечения делятся пополам.
⇒ - параллелограмм.
⇒ ед., и
ед., по свойству параллелограмма.
ед.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.
⇒ ед.
ед.
ед.
Ответ:
Условие не полное, но судя по рисунку - задачи из темы "равнобедренные треугольники" и опять же из рисунка напрашивается, что BC=AC=8. В предположении, что это действительно так, даю ответ в приложении. Только если этот вопрос не из популярных, то делаю это я напрасно.
Объяснение:
