Предмет: Геометрия,
автор: yanagorockevich
Дан равнобедренный треугольник ABC с основанием AC, у которого BC = 8 см, угол A : углу B = 1 : 4. Найдите площадь треугольника ABC.
Ответы
Автор ответа:
8
Ответ:
16√3 см²
Объяснение:
Дано: ΔАВС - равнобедренный, ВС=АВ=8 см.
∠А/∠В=1/4.
Найти S(АВС).
Пусть ∠А=∠С=х° т.к. у равнобедренного треугольника углы при основании равны
Тогда ∠В=4х°.
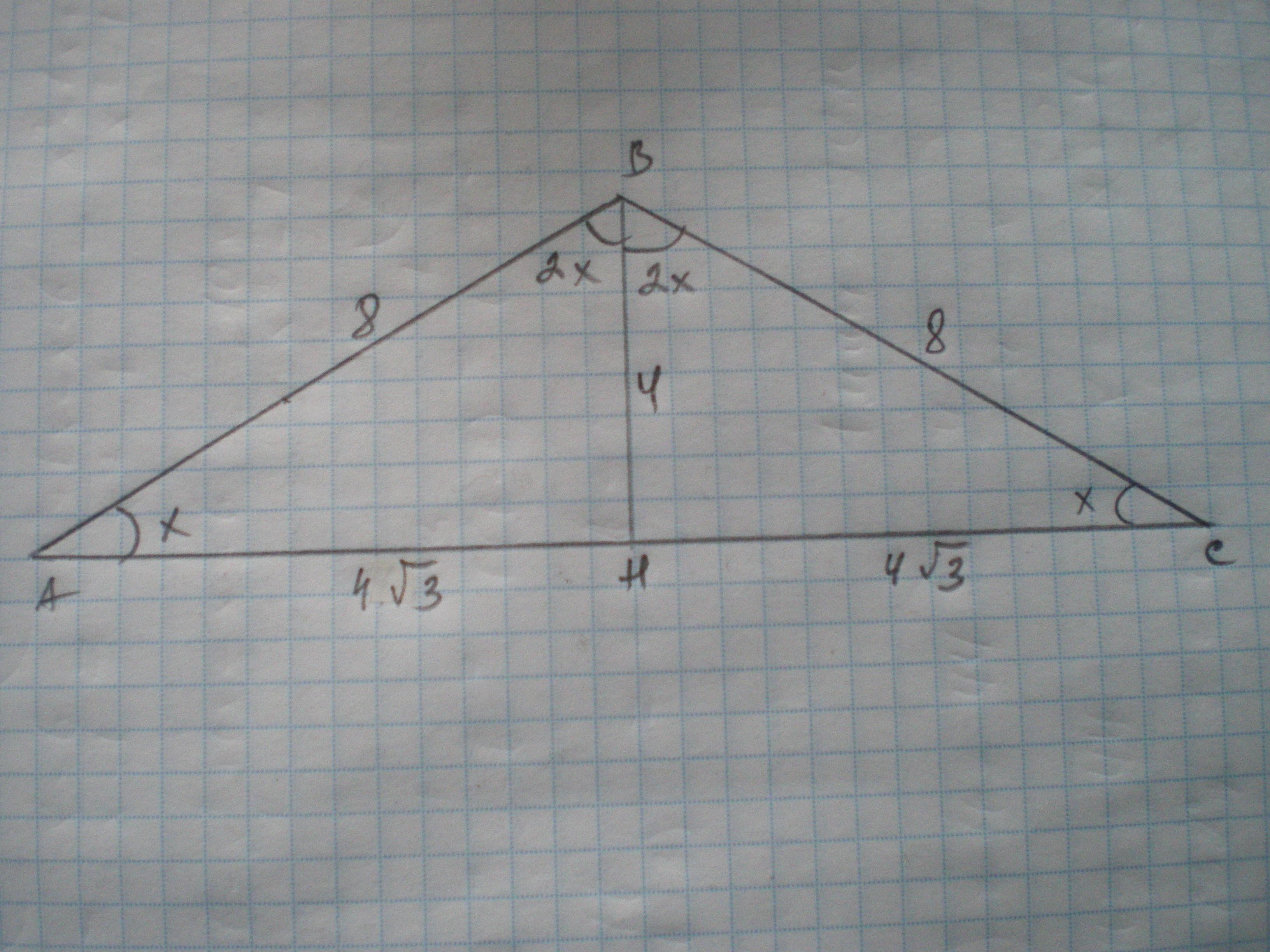
Проведем высоту ВН, которая является и биссектрисой ∠В по свойству высоты равнобедренного треугольника.
Тогда ∠АВН=1/2 ∠В=2х°
Рассмотрим ΔАВН - прямоугольный, ∠А+∠АВН=90° по свойству острых углов прямоугольного треугольника. Составим уравнение:
х+2х=90; 3х=90; х=30. ∠А=30°, тогда ВН=1/2 АВ = 8:2=4 см по свойству катета, лежащего против угла 30 градусов.
По теореме Пифагора АН=(√АВ²-ВН²)=√(64-16)=√48=4√3 см.
АС=2 АН=4√3 * 2 = 8√3 см
S(АВС)=1/2 * АС * ВН = 1/2 * 8√3 * 4 = 16√3 см²
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: zkarylkasynkarakat
Предмет: Математика,
автор: aiteevablai
Предмет: Литература,
автор: vlasenkoliza2018
Предмет: Литература,
автор: Аноним
Предмет: Литература,
автор: бананчик1123