Question

На острове живут рыцари которые всегда говорят правду и лжецы которые всегда лгут. однажды встретились трое островитян: джон, джим и джек.
-джим может сказать что джек лжец,-заявил джон

-джек может сказать что джон лжец,- заявил джим

-джон может сказать что джим лжец,-заявил джек.

сколько рыцарей среди них может быть? (укажите все возможные варианты)

ПОМОГИТЕ ПЖПЖПЖ!!! МНЕ СРОЧНО НУЖНО!

Answer 1

Ответ:

0 рыцарей или 2 рыцаря

Пошаговое объяснение:

    Поскольку не указано число верных фраз или других указаний в условии, то предполагаем, что каждый из троих может быть или рыцарем или лжецом .

1). "- Джим может сказать, что Джек лжец, - заявил Джон".

 Если Джон рыцарь, то его высказывание  - истина независимо от статуса других островитян.  

Джим может быть также рыцарем, тогда Джек действительно лжец. Т.е. в этом варианте 2 рыцаря (Джон и Джим) и 1 лжец (Джек).

Если Джим лжец, тогда Джек  - рыцарь . И здесь 2 рыцаря (Джон и Джек) и 1 лжец (Джим).

  Если Джон лжец, то Джим не может назвать Джека лжецом, т.к. Джон не может сказать правду. Т.е. Джим скажет, что Джек рыцарь.

Если Джим рыцарь, то это - правда, и в этом варианте также 2 рыцаря (Джим и Джек) и 1 лжец (Джон).

Если Джим лжец, то его словам, что Джек рыцарь, нельзя верить: Джек тоже лжец. В этом варианте все трое - лжецы.

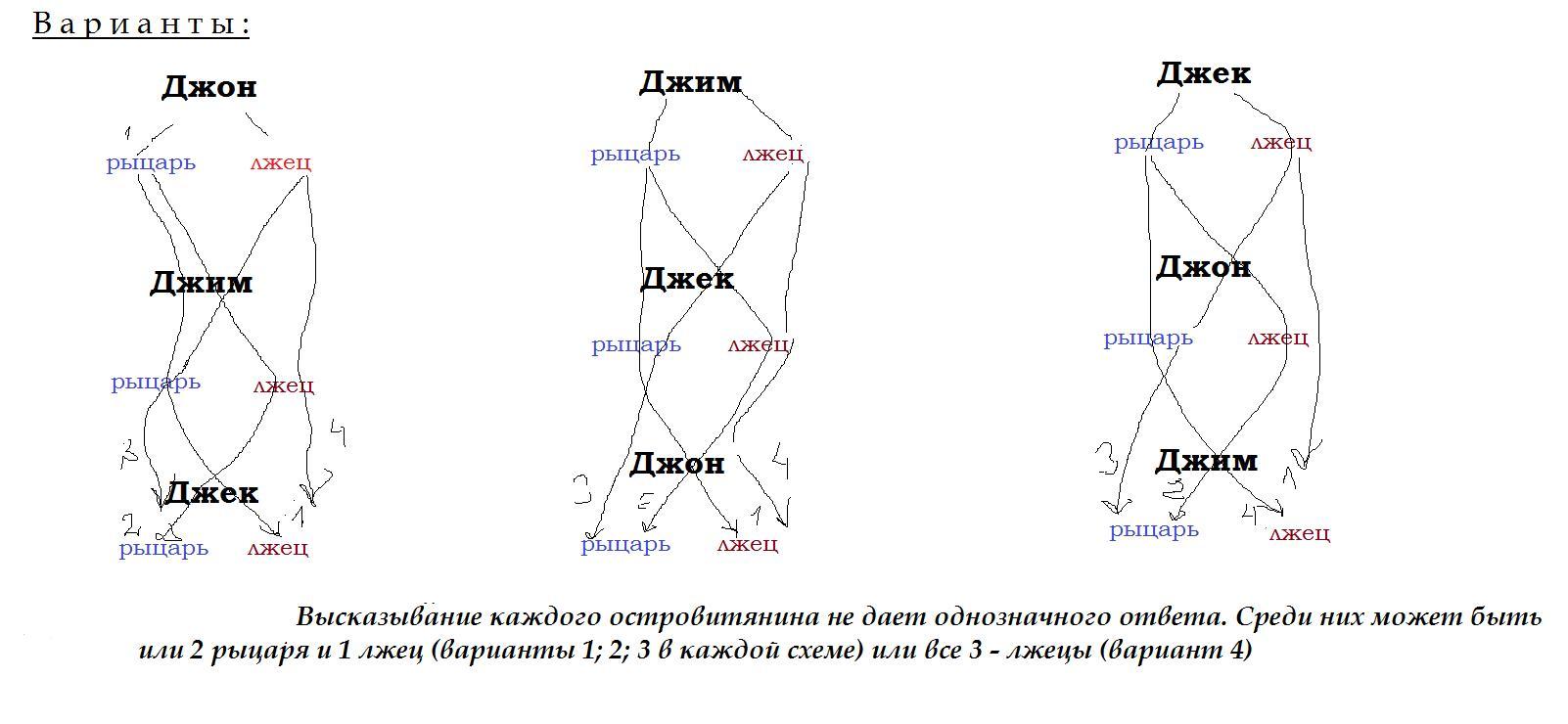
2). По другим высказываниям рассуждения аналогичные, приводящие к тем же вариантам – 2 рыцаря и один лжец или 3 лжеца, только имена лжецов и рыцарей различны. Схемы даны в приложении.

3). Истинный статус каждого  по данным условия установить нельзя, да и задание требует только назвать количество рыцарей. Из всех схем можно сделать вывод, что кроме 0 или 2 рыцарей других вариантов нет.

Ответ: 0 рыцарей или 2 рыцаря.