Question

Интересная задача
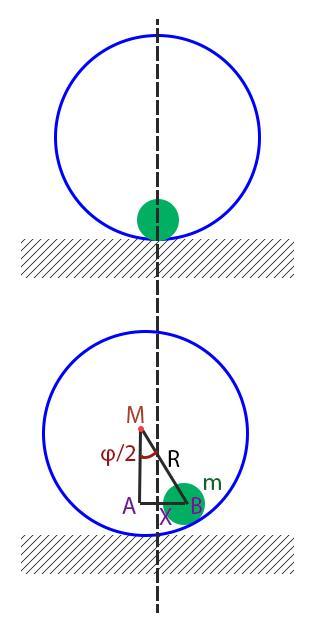
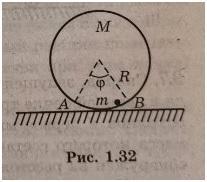
На столе находится сфера радиусом R = 1,2 м и массой М = 4 кг, внутри которой катается маленький металлический шарик массой m = 2 кг (рис. 1.32). Какова амплитуда колебаний центра сферы, если шарик катается между точками А и В в пределах угла φ = 60°? Трением пренебречь.

Answer 1

Ответ:

0,2 м

Объяснение:

Центр масс не должен двигаться "по горизонтали".

Сферу можно заменить массой M на высоте R.

Зафиксируем положение центра масс системы в момент, когда шарик проходит положение равновесия (верхний рисунок). Центры масс сферы и шарика находятся на пунктирной прямой, тогда и сам центр масс системы находится на ней.

Рассмотрим крайнее положение шарика (нижний рисунок). Шарик сдвинулся вправо от положения центра масс, тогда сфера сдвинулась влево. Проведем отрезок из центра сферы в центр шарика: шарик маленький, так что можно думать, что длина этого отрезка равна радиусу сферы; кроме того, проведем вертикальную прямую в нижнюю точку сферы. Достраиваем до прямоугольного треугольника, катет AB лежит напротив угла в 30°, значит, он равен половине гипотенузы, AB = R/2.

Точка X делит отрезок AB в некотором отношении. Точку X можно найти по правилу рычага:

$M\cdot AX=m\cdot XB\\M\cdot AX=m\cdot(AB-AX)\\(M+m)\cdot AX=m\cdot AB=\dfrac{mR}{2}\\AX=\dfrac12\cdot\dfrac{m}{M+m}R$

AX – расстояние, на которая сфера сдвигается, если шарик находится в крайнем правом положении. Очевидно, если шарик находится в крайнем левом положении, расстояние будет таким же, а тогда амплитуда равна AX.

$AX=\dfrac12\dfrac{m}{M+m}R=\dfrac{2}{2\cdot(4+2)}\cdot1.2\text{ m}=\dfrac{1.2\text{ m}}6=0.2\text{ m}$