Предмет: Геометрия,
автор: batmangirl
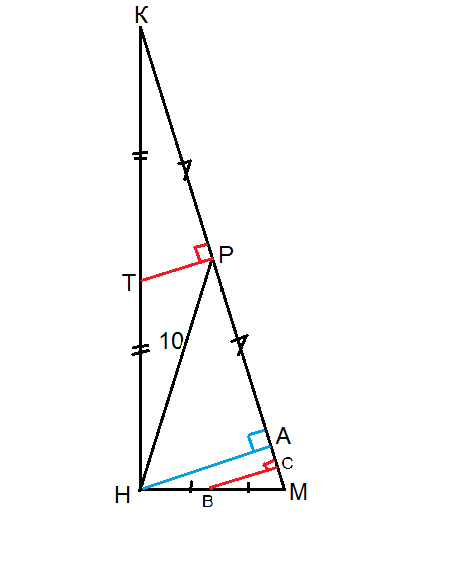
В прямоугольном треугольнике КМН медиана НР=10, а его площадь равна 280 см в квд. найдите расстояние от середины катета НК до гипотенузы КМ.
Ответы
Автор ответа:
0
Прошу модераторов не удалять задачу. Условие в ней дано с ошибкой. Причем эта задача даже на учительском ресурсе Фестиваль дана с таким же ошибочным условием.
Т.к. медиана прямоугольного треугольника, проведенная из прямого угла к гипотенузе, равна половине гипотенузы, то гипотенуза равна 2*10=20 см.
Если из площади находить высоту этого треугольника по формуле
S=a*h:2, то
h= 2S:а
h=560:20=28 см при том, что гипотенуза равна 20, чего не может быть.
---------------
При площади данного треугольника равной 28 см²
h=56:20=2,8 см
Тогда неважно, какой катет будет избран для того, чтобы определить расстояние от его середины до гипотенузы.
Искомое расстояние ( см. рисунок) ВС в треугольнике НАМ или ТР в треугольнике КАН будет равным половине высоты, проведенной из прямого угла к гипотенузу КМ, т.к. является средней линией каждого из этих треугольников.
Т.е. расстояние от середины любого катета до гипотенузы равно
2,8:2=1,4 см
Т.к. медиана прямоугольного треугольника, проведенная из прямого угла к гипотенузе, равна половине гипотенузы, то гипотенуза равна 2*10=20 см.
Если из площади находить высоту этого треугольника по формуле
S=a*h:2, то
h= 2S:а
h=560:20=28 см при том, что гипотенуза равна 20, чего не может быть.
---------------
При площади данного треугольника равной 28 см²
h=56:20=2,8 см
Тогда неважно, какой катет будет избран для того, чтобы определить расстояние от его середины до гипотенузы.
Искомое расстояние ( см. рисунок) ВС в треугольнике НАМ или ТР в треугольнике КАН будет равным половине высоты, проведенной из прямого угла к гипотенузу КМ, т.к. является средней линией каждого из этих треугольников.
Т.е. расстояние от середины любого катета до гипотенузы равно
2,8:2=1,4 см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: vladbekobad03
Предмет: Математика,
автор: kazan144
Предмет: Химия,
автор: Nikitamel228822
Предмет: Алгебра,
автор: b1p