Предмет: Математика,
автор: matweio
На стороне AD квадрата ABCD отметили точку K, а на продол- жении луча AB за точку B — точку L. Известно, что ∠LKC = 45◦, AK = 1, KD = 2. Найдите LB.
Приложения:

Аноним:
LB = 2
Ответы
Автор ответа:
14
LC - расстояние от точки L к CL, ∠ LCK = 90°. Рассмотрим прямоугольный треугольник CKD, по т. Пифагора:
Поскольку ∠LKC = ∠KLC , то ΔLKC - равнобедренный прямоугольный треугольник ⇒ CK = CL = √13. Тогда по теореме Пифагора из прямоугольного треугольника LBC:
Ответ: 2.
Приложения:
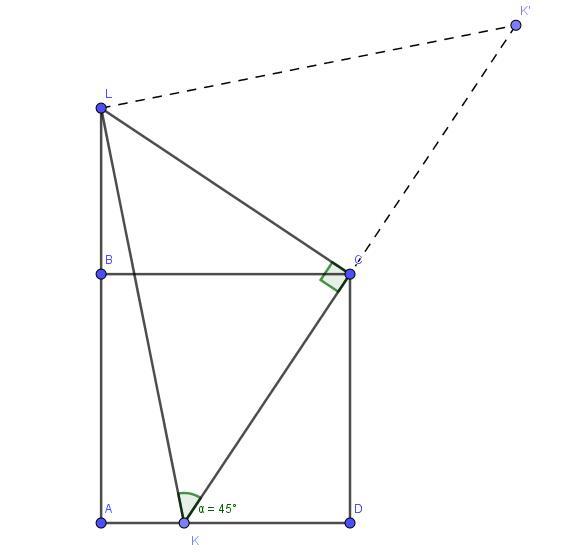
А почему LCK=90? Как обосновать?
LC - серединный перпендикуляр
точка K' это симметричная точка относительно точки С, т.е. треугольник LKK' - РП равнобедренный и точка С - середина КК'
Похожие вопросы
Предмет: История,
автор: 0r0i0n0a0
Предмет: Литература,
автор: igrvurxitfitothug
Предмет: Физика,
автор: 2007505
Предмет: Алгебра,
автор: NYANcrezy
Предмет: Математика,
автор: Аноним