Предмет: Математика,
автор: Aimer7
lim x->+oo ((x^3)-(x^2))/(((-2+x)^3)-x^3)
Требуется решить такой предел
Результат получается 1/oo
Но онлайн калькуляторы утверждают, что ответ -oo
Почему ?
Приложения:
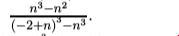
igorShap:
А как Вы получили 1/oo?..
Ответы
Автор ответа:
1
Т.к.
, то
Похожие вопросы
Предмет: Музыка,
автор: Chpunchik
Предмет: Математика,
автор: batonyjery
Предмет: Қазақ тiлi,
автор: bekzat787ghg
Предмет: Математика,
автор: джедин
Предмет: Математика,
автор: aza68