Предмет: Математика,
автор: mmmic
Помогите
Докажите неравенства
Приложения:
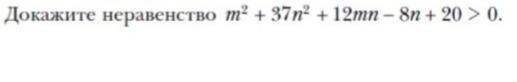
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Выделим полные квадраты:
Любое действительное число в квадрате всегда больше либо равно нулю! А если еще и прибавить положительное число, то результат будет строго больше нуля!
То есть, если (m+6n)²≥0 и (n-4)^2≥0, тогда (m+6n)²+(n-4)²+4>0 - ч.т.д
P.S. также можно сказать, что наименьшее значение этого выражения равно 4
Похожие вопросы
Предмет: Қазақ тiлi,
автор: tursynbayraiana
Предмет: Қазақ тiлi,
автор: shtifrudolf
Предмет: Русский язык,
автор: amina12337795
Предмет: Математика,
автор: zhuzi13700
Предмет: Математика,
автор: theleno4ka