Question

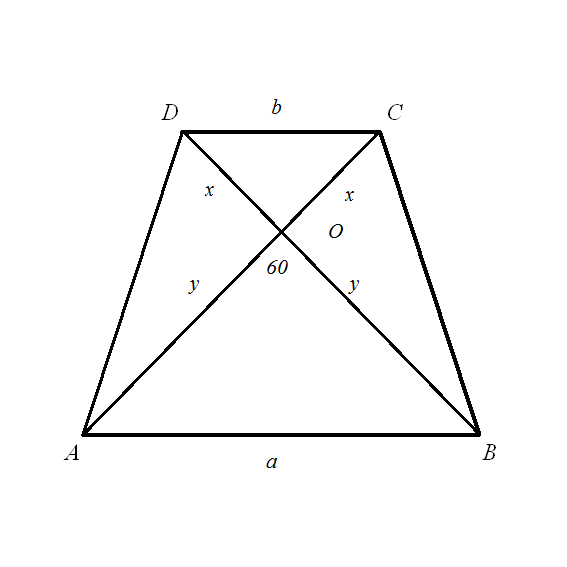
в не которой трапеции длина одной из диагоналей равна сумме  длин основной трапеции, а угол между диагоналями равен 60 градусов. доказать, что эта трапеция равнобокая.

Answer 1

От противного. Предположим, что трапеция равнобедренная:
AO=OB=y(по свойствам трапеции)
В треугольнике AOB по теореме косинусов:
$a^2=y^2+y^2-2y*y*cos60\ cos 60=0.5\ a^2=2y^2-y^2\ a^2=y^2\ a=y$
OD=OC=x
В треугольнике DOC по теореме косинусов:
$b^2=2x^2-2x^2*cos60\ b^2=2x^2-x^2=x^2\ b=x$
a=y и b=x, тогда диагональ d=b+a(подтверждаем условие)
Треугольники DOC и AOB - правильные, т.к a=y=y и b=x=x, тогда их углы равны по 60.
Рассмотрим треугольники DBA и ACB, 
x+y=x+y, следовательно ВD=AC, AB - общая, углы DBA и CAD равны по 60, следовательно треугольники равны, следовательно DA=CB, следовательно трапеция - ранобедренная