Предмет: Математика,
автор: Amandee
(((((КТО СМОЖЕТ РЕШИТЬ, ПОЖАЛУЙСТА СРОЧНО РЕШИТЕ!!!!!!!
Приложения:
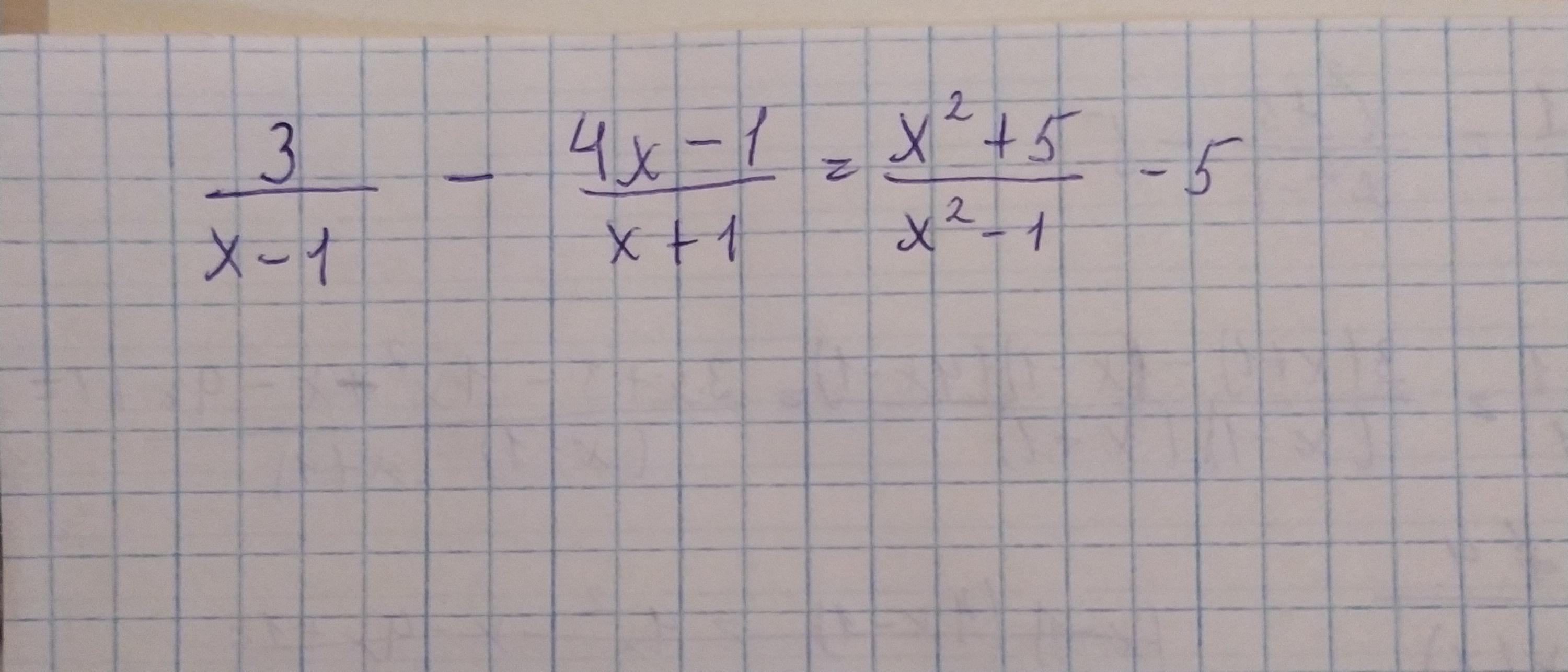
Ответы
Автор ответа:
1
Пошаговое объяснение:
ОДЗ
x ≠ 1
x ≠ -1
x = 1 не подходит по ОДЗ
Ответ: не имеет решений.
Похожие вопросы
Предмет: Математика,
автор: ivankohannyj4
Предмет: Қазақ тiлi,
автор: saimongame
Предмет: Другие предметы,
автор: Hashirama5464
Предмет: История,
автор: вдудв