Срочно
Две прямые с уравнениями 2x-y+2=0 и 2x-y-6=0 образуют прямоугольник с диагональю x-y+2=0 найти две другие стороны
Ответы
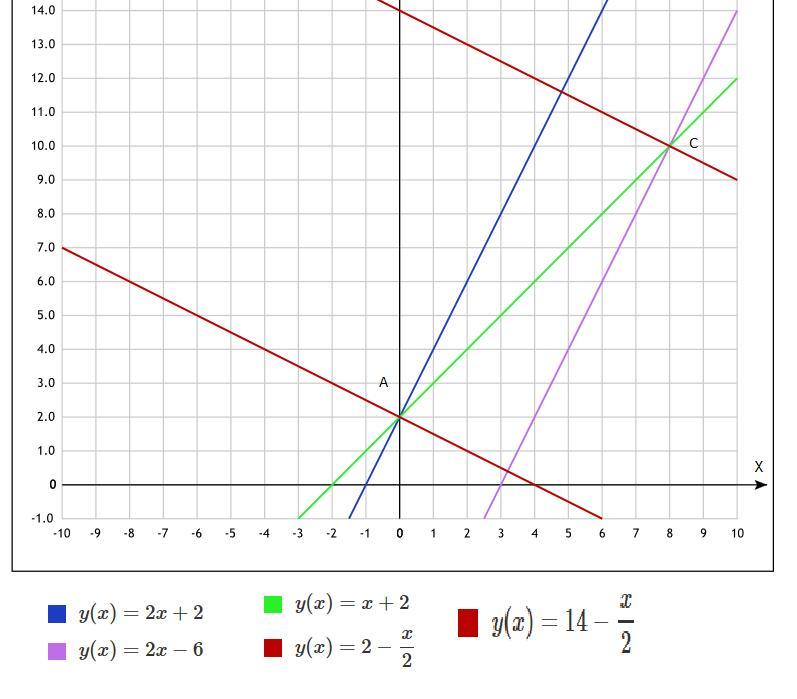
1)найду вершины прямоугольника-точки пересечения диагонали с заданными прямыми. Для этого надо решить 2 системы уравнений
а) 2x-y+2=0 и x-y+2=0
y=2x+2; x-2x-2+2=0; x=0;y=2-первая, пусть будет А(0;2)
б)2x-y-6=0 и x-y+2=0
y=2x-6; x-2x+6+2=0; x=8; y=10-пусть будет С(8;10)
2)к первой прямой из точки А ищу нормаль,это n1(2;-1)
n1 и нормаль искомой стороны n2 (x1;y1) перпендикулярны. значит скалярное произведение их должно быть 0
тогда оно в координатах (n1,n2)=2*x1-1*y1=0; тогда x1=1; y1=2
(1;2) нормаль искомой прямой n2, тогда уравнение искомой прямой x+2y+c=0; Эта прямая проходит через точку A, подставив ее нахожу c
0+2*2+c=0; c=-4
Тогда уравнение третьей стороны прямоугольника x+2y-4=0
Вторая искомая сторона параллельна первой искомой, поэтому просто найду С1, подставив точку С в уравнение x+2y+c=0
8+2*10+c1=0; c1=-28
тогда уравнение второй искомой стороны
x+2y-18=0