Предмет: Алгебра,
автор: kirill89828
ПОЖАЛУЙСТА ОЧЕНЬ НУЖНО!!! задание в фото
Приложения:
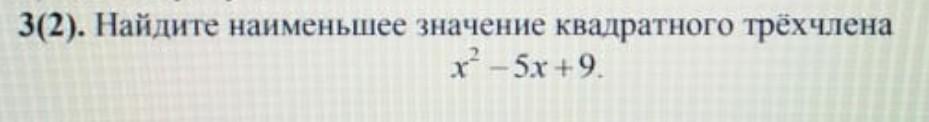
Ответы
Автор ответа:
0
Для нахождения минимального значения функции y(x) = x^2-5x+9 , нужно :
1) Взять производную от (x^2-5x+9)* ( * - значит берем производную ) = 2x-5
2)Решить уравнение 2x-5 = 0 , x = 2.5
3)Проверить является данное значение аргумента локальным минимум или максимом ,для этого возьмем производную второго порядка,т.е. (2x-5)* =2,значит функция не имеет наибольшего значения ,тогда x=2.5 - локальный минимум функции ,значение функции в точке x = 2.5 ,y = 2.75
Ответ : 2.75
kirill89828:
а путём формулы сокращённого умножения?
К сожалению, ничего сказать не могу , я все через производную считаю
пасиб
а ты какой класс
9?
10 :)
ну тогда понятно, я это уже изучил, но учитель говорит через ФСУ, а я не помню
8 класс
)))
Похожие вопросы
Предмет: География,
автор: schoollifee5
Предмет: Математика,
автор: timurgarifulin160
Предмет: Алгебра,
автор: 111Zorro111
Предмет: Алгебра,
автор: lizz33419724