Предмет: Математика,
автор: Funtntd
помогите упростить выражение
Приложения:
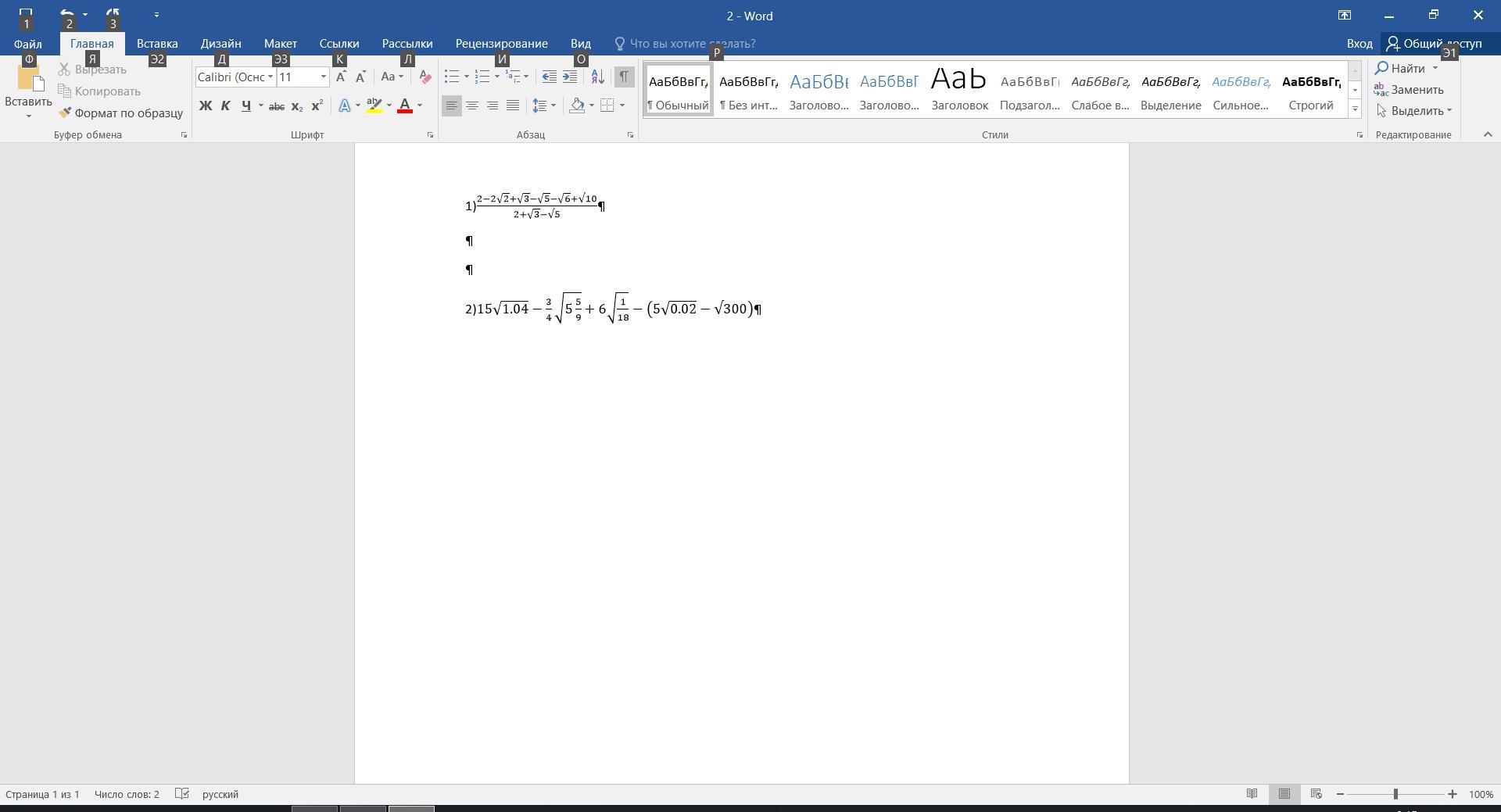
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
=
==
==
==
=
=
==
==
==
=
=
==
==
==
==
=
kuponr:
добавил в решение
а где искать?
ага обновил
и появилось
огромное вам спасибо,можно будет к вам обращаться если,что?
Я не часто за компом бываю, в основном после полуночи на пару часиков
да и мне редко бывает нужна помощь такого рода,но бывает
ещё раз спасибо
удачи!
взаимно
Автор ответа:
0
Ответ: во вложении Пошаговое объяснение:
Приложения:
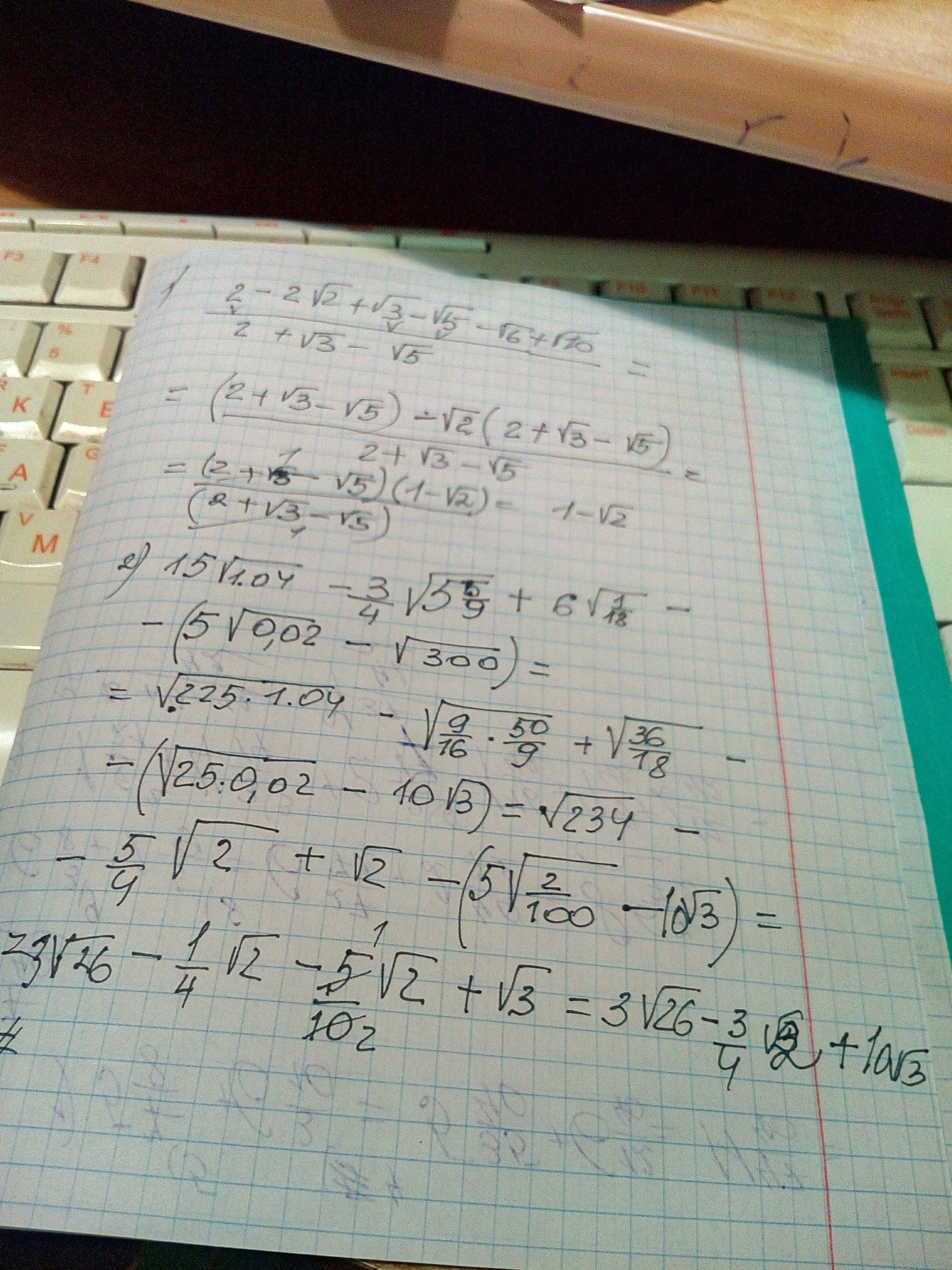
ясен пень
Похожие вопросы
Предмет: Английский язык,
автор: daukazhunis
Предмет: Английский язык,
автор: kcernaga
Предмет: Математика,
автор: alekseewaekaterina12
Предмет: Математика,
автор: alice79
Предмет: Литература,
автор: KrYtOu008