Исследуйте функцию и постройте её график.
y=x^4+x^3-x^2
Ответы
ДАНО: y(x) = x⁴ + x³ - x²
Думаем: Парабола четвёртой степени и немного кривая.
ИССЛЕДОВАНИЕ
1. Область определения. Непрерывная. Разрывов нет.
D(x) = (-∞;+∞)
2. Корни функции: х₁ = - 1,618, х₂ = х₃ = 0 и х₄ = 0,618.
Нахождение самих корней - без комментариев. ДВА корня равны 0..
3. Интервалы знакопостоянства.
Положительна: Y>0 X∈(-∞;-1.618)∪(0.618;+∞) - вне корней.
Отрицательна: Y<0 X∈(-1.618;0,618) - между корней.
4. Поиск экстремумов по первой производная функции .
Y'(x) = 4*x³ +3*x² -2 = 0
. Решалось по теореме Виета.
Точки экстремумов: x₅ = - 1,175, x₆ = 0, x₇ = 0,425
5 Локальные экстремумы:
Ymin(х₅=-1,175) = - 1,10 Ymax(х₆= 0 ) = 0, Ymin(x₇=0.425) = -0.07
6. Интервалы монотонности.
Убывает: Х∈(-∞;x₅=-1.175)∪(x₆=0;x₇=0.425)
Возрастает: Х∈(-1.175;0)∪(0.425;+∞)
7, Поиск точек перегиба по второй производной
Y"(x) = 12*x² +6х -2 = 0
. Парабола. D=132, √132≈ 11.5
x₈ =-0,73 и х₉ = 0.23 - точки перегиба.
8. Поведение функции.
Вогнутая - "ложка" - Х∈(-∞;х8=-0,73)∪(х9=0,23;+∞) - вне корней параболы.
Выпуклая - "горка" - Х∈(х₈=-0,73);(х₉=0,23)) -между корнями параболы.
9. Область значений.
E(y) ={Ymin(x₅=-1.175);+∞}
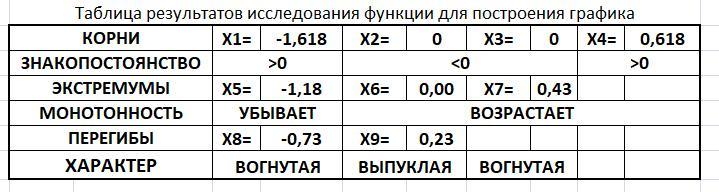
10. Таблица с результатами в приложении.
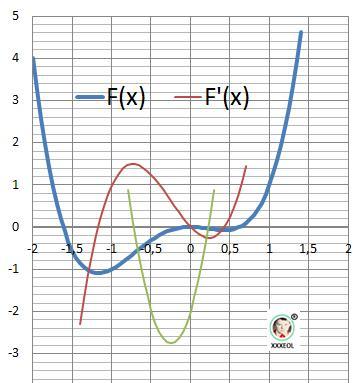
11. Графики всех функций на рисунке в приложении.
Они, конечно , излишни, но наглядно показывают причины преобразования функции. Второй минимум показать конечно сложно.