Предмет: Геометрия,
автор: 13valeria13
Бисектриса кута D Прямоугольника АВСD делит сторону ВС в точке М, ВМ:МА=5:3. Найдите стороны прямоугольника если его периметр равен 66 см
Ответы
Автор ответа:
2
Ответ:
9 см, 9 см, 24 см, 24 см.
Объяснение:
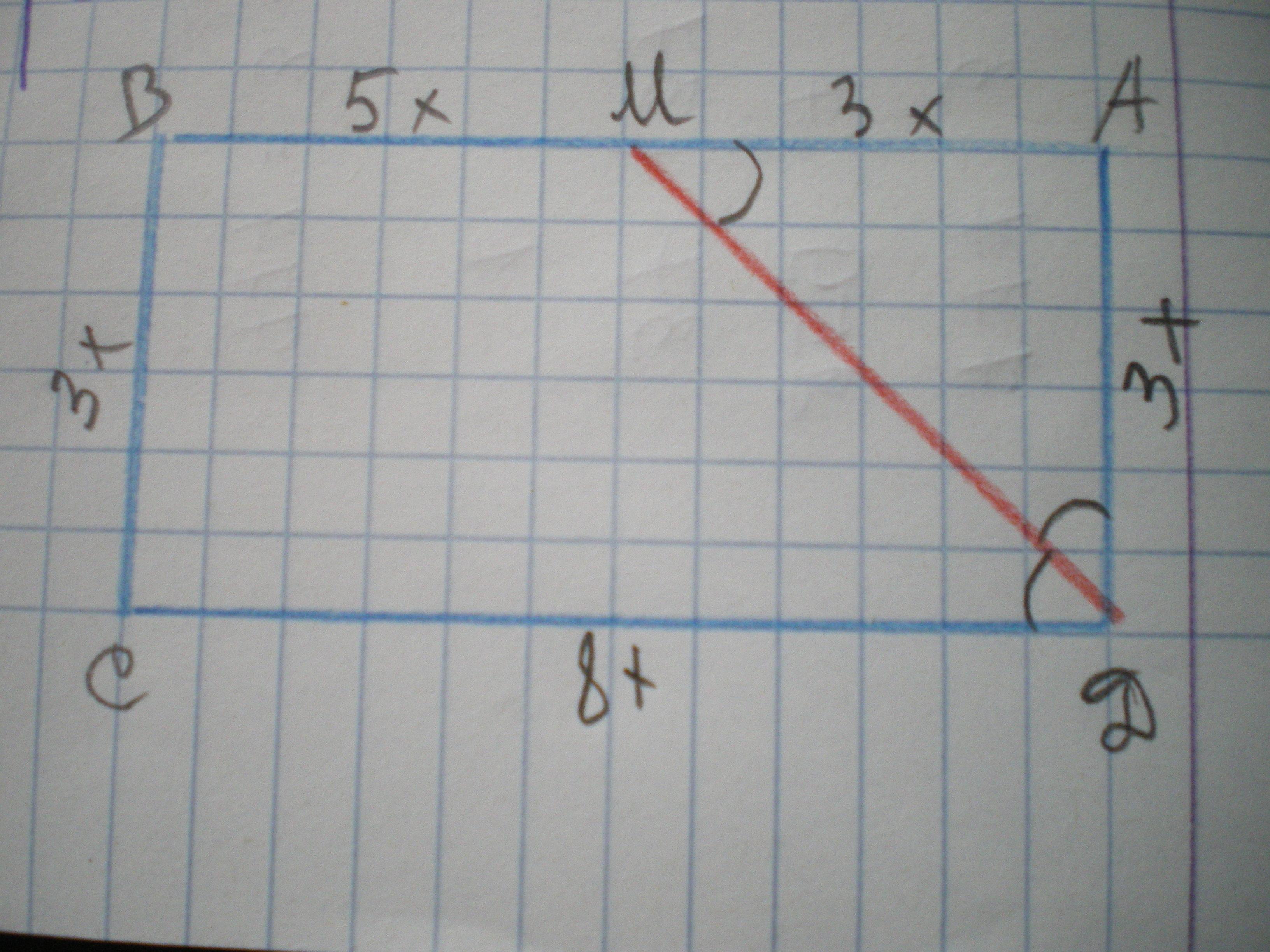
Дано: АВСD - прямоугольник, DМ - биссектриса, ВМ:МА=5:3. Р(АВСD)=66 см. Найти АВ, ВС, СD, AD.
АВ=СD, AD=ВС по свойству сторон прямоугольника.
∠ADM=∠CDM по определению биссектрисы
∠AMD=∠CDM как внутренние накрест лежащие при АВ║CD и секущей MD
∠AMD=∠ADM, следовательно, ΔADM - равнобедренный, АМ=DM.
Пусть ВМ=5х см, АМ=ВС=AD=3х см, CD=AB=3x+5x=8x см.
Составим уравнение: (3х+8х)*2=66
22х=66; х=3.
AD=BC=3*3=9 см
AB=CD=8*3=24 см
Приложения:
Похожие вопросы
Предмет: Математика,
автор: dimaekspert831
Предмет: Математика,
автор: dimaekspert831
Предмет: Русский язык,
автор: sofiaorlovaomsk11
Предмет: Математика,
автор: mishella
Предмет: История,
автор: ДашаПортняша