Предмет: Геометрия,
автор: Smouki
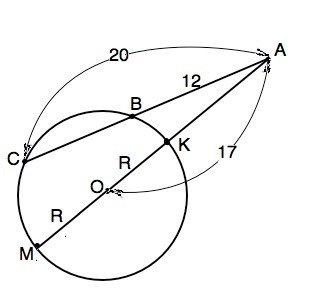
Из точки вне окружности проведена секущая, пересекающая окружность в точках, удалённых от данной на 12 см и 20 см. Расстояния от данной точки до центра окружности равно 17 см. Найдите радиус окружности.
Ответы
Автор ответа:
0
На рисунке в приложении точка вне окружности – А. Продлим АО до пересечения с дальней стороной окружности в точке М. Имеем две секущие 1) АС=20 см, внешняя ее часть АВ=12 см. 2) АМ=17+R, внешняя часть АК=17-R. По теореме о секущих: Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. ⇒ АВ•АС=АК•АМ, откуда 12•20=(17+R)•(17-R) ⇒ 240=289-R² ⇒, R=√(289-240)=7 см
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Stelene12
Предмет: Алгебра,
автор: levgrusha
Предмет: Математика,
автор: pavlovskaazlata
Предмет: Математика,
автор: Natali1982