Предмет: Алгебра,
автор: ZzzauchKa
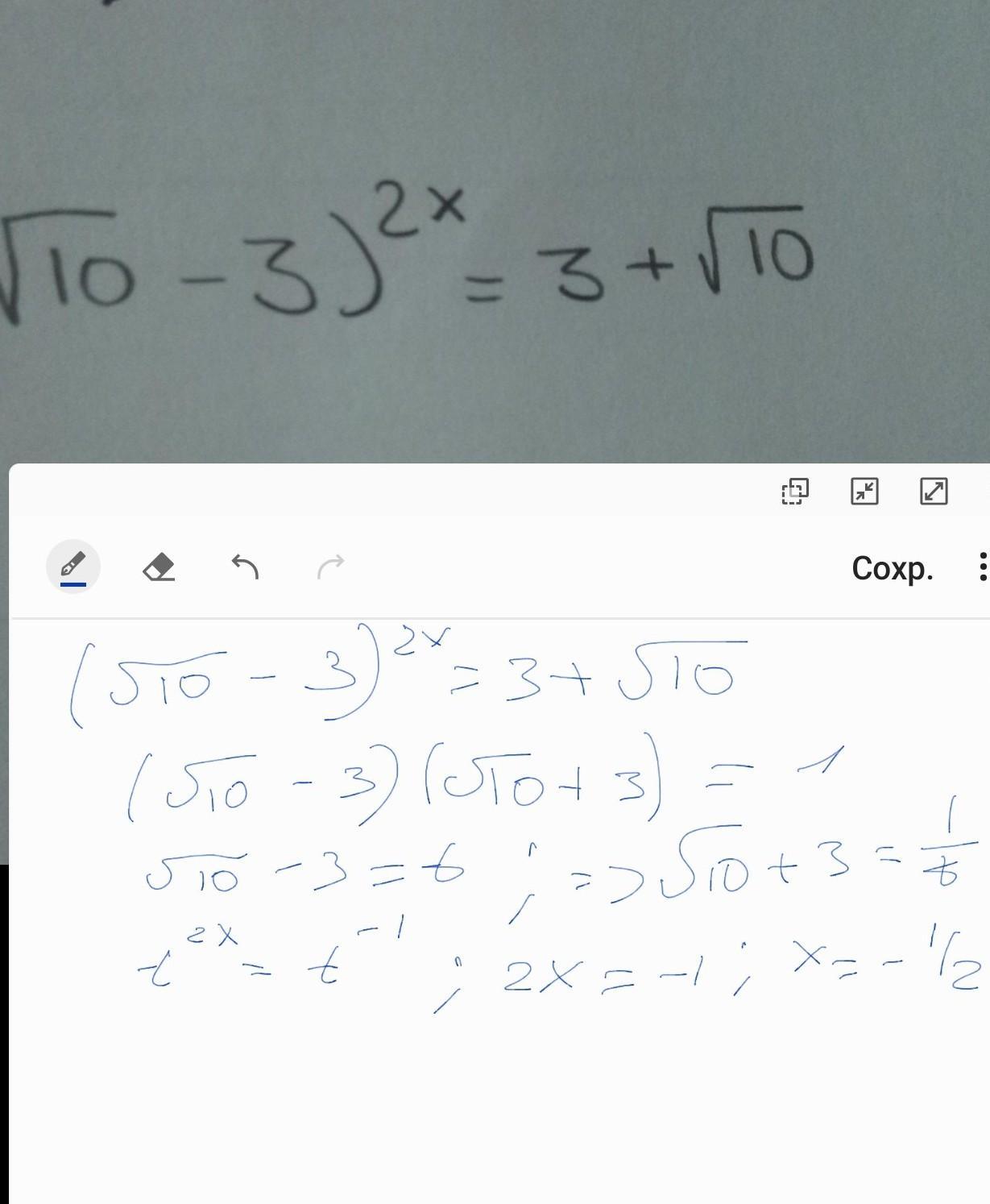
(√10-3)^2x=3+√10.........
Приложения:

Ответы
Автор ответа:
0
Ответ:
.............................
Приложения:
genius20:
Да, у вас решение проще, а я что-то намудрил)
Автор ответа:
0
Проверим, не являются ли числа и
взаимно обратными (уж очень похоже):
Чтобы избавиться от иррациональности в знаменателе, умножим и числитель, и знаменатель на сопряжённое знаменателю выражение:
Ура! Эти числа взаимно обратны. Запишем ещё раз:
Тогда получим, что
Ответ:
P. S. Наверняка есть решение более логичное и строгое, а у меня получилось начало решения скорее интуитивное, т. к. уже решал подобные примеры.
Похожие вопросы
Предмет: Русский язык,
автор: holdik3949449
Предмет: Математика,
автор: amxxz
Предмет: Математика,
автор: andrejgilgenberg4
Предмет: Химия,
автор: сашаСталь