Предмет: Геометрия,
автор: vozniukvika21
Запиши уравнение круга радиусом кореня из 5, если его центр лежит на биссектрисе первого координатной четверти. которое проходит через точку (2;5).
Ответы
Автор ответа:
1
Ответ:
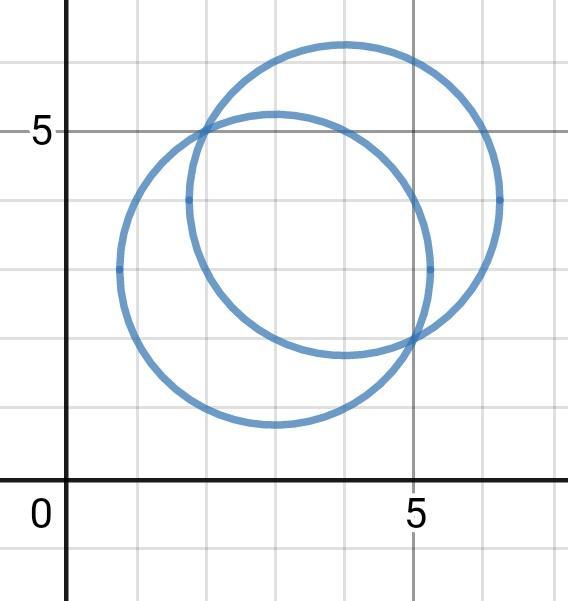
(х-3)^2 + (у-3)^2 = 5
(х-4)^2 + (у-4)^2 = 5
Объяснение:
уравнение окружности с центром (х0; у0) радиуса r
(x-x0)^2 + (y-y0)^2 = r^2
r^2 = 5 (по условию)
точки, лежащие на биссектрисе 1 координатной четверти, удовлетворяют условиям
у=х, у>0, х>0
т.е. у нас х0=у0
(х-х0)^2 + (у-х0)^2 = 5
осталось подставить координаты точки х=2; у=5
(2-х0)^2 + (5-х0)^2 = 5
2*(х0)^2 - 14х0 + 29-5 = 0
(х0)^2 - 7х0 + 12 = 0
корни по т. Виета (3) и (4)
получилось два решения
(х-3)^2 + (у-3)^2 = 5
(х-4)^2 + (у-4)^2 = 5
Приложения:
Похожие вопросы
Предмет: География,
автор: sgod8720
Предмет: Литература,
автор: armanevabudabi
Предмет: Английский язык,
автор: babyVENERA
Предмет: Математика,
автор: madamoksanaru