Предмет: Математика,
автор: Sp1ceGood
Посчитать 
Ответы
Автор ответа:
1
Ответ:
............................
Приложения:
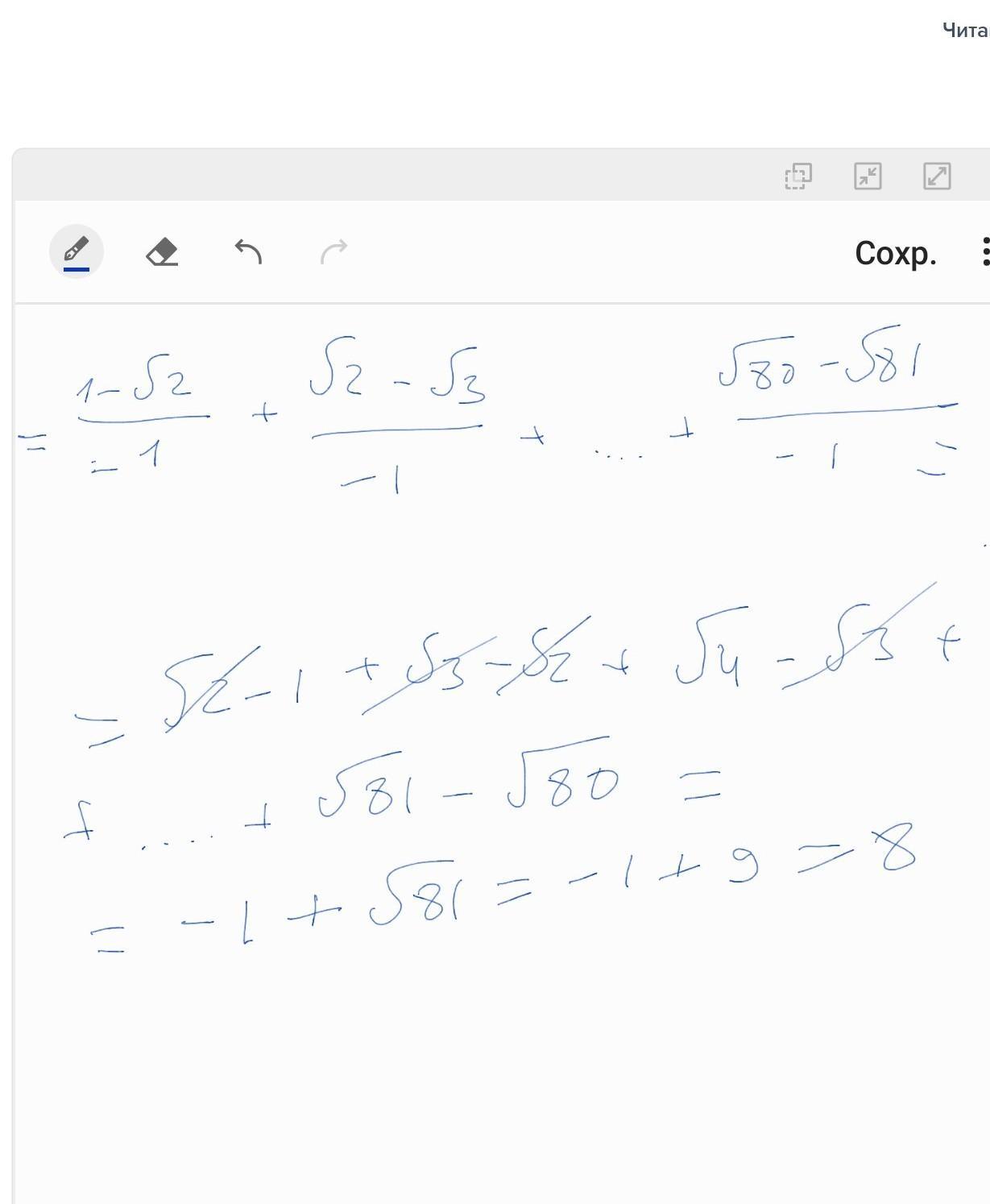
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: genagewa
Предмет: Английский язык,
автор: Politelenovayz
Предмет: Алгебра,
автор: ViiiTta
Предмет: Математика,
автор: инна313
Предмет: Математика,
автор: никол77