Предмет: Алгебра,
автор: tarshilov05
Вот решите прошу данное задание, а то это не возможно, просто я сидел думал весь вечер, так и не решил, это единственное задание которое я не смог сделать, даю 20 баллов
Приложения:

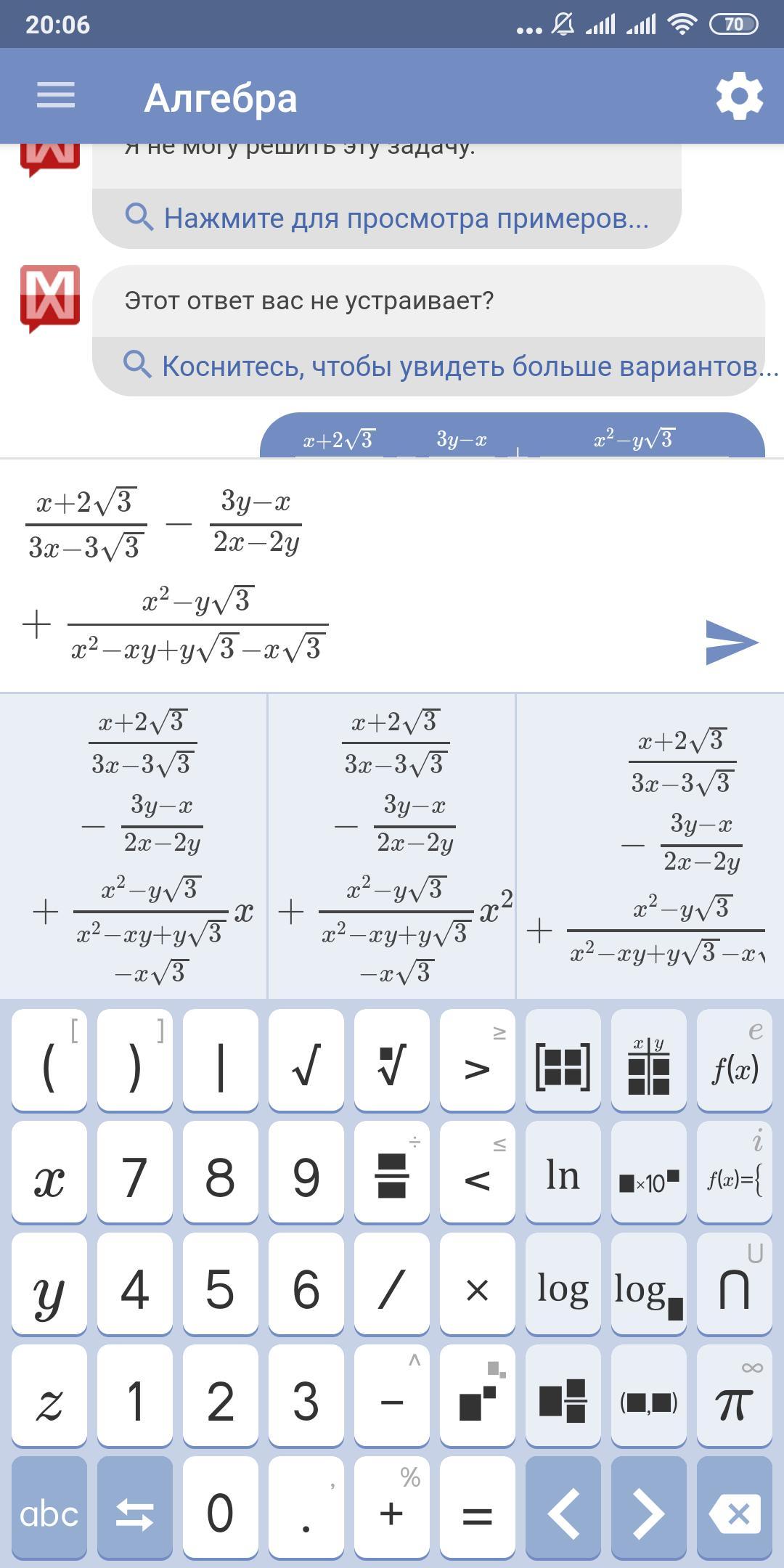
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: timyrgyrskiy
Предмет: Биология,
автор: SUPERFUN14
Предмет: Физика,
автор: IvanKlimov2006
Предмет: История,
автор: 2468105
Предмет: Математика,
автор: Аноним