Предмет: Алгебра,
автор: вкпа
15 БАЛЛОВ! Два действительных числа случайным образом выбираются из отрезка [0,6]. Какова вероятность того, что сумма двух чисел меньше 5, а их произведение меньше 6? решать с помощью геометрического определения вероятности
Аноним:
(5+3ln(3/2))/18
Ответы
Автор ответа:
3
Пусть х - первое число, у - второе число. По условию, откуда
и
откуда
Найдем точки пересечения графиков функций и
. Для этого приравниваем функции
По теореме Виета
Смотрим рисунок. Разобьем заштрихованную фигуру прямыми x = 2 и x = 3 и найдем площади
кв. ед.
кв. ед.
кв. ед.
Площадь заштрихованной фигуры:
Искомая вероятность:
Приложения:
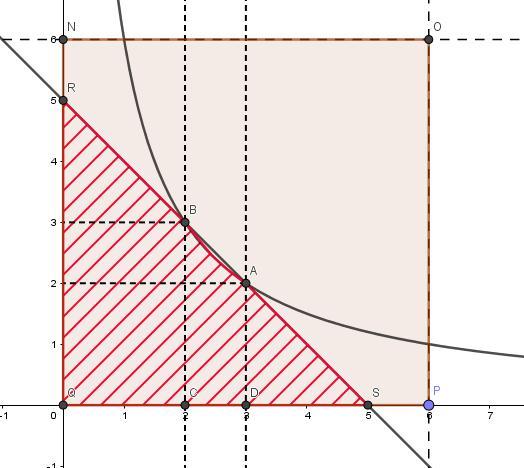
Спасибо!
Похожие вопросы
Предмет: Физика,
автор: hrustalevigor05
Предмет: Математика,
автор: xxsd0908
Предмет: Українська мова,
автор: npilipcuk616
Предмет: Литература,
автор: knopik8989