Предмет: Математика,
автор: andrewsib9
Найти область сходимости степенного ряда
Приложения:
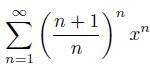
Simba2017:
наверное при х меньше 1
Был бы очень благодарен, если написали решение
я такие не решаю, есть здесь специалисты, но не знаю помогут ли...
вы то сами никому не помогли
Ответы
Автор ответа:
2
А значит при ряд сходится.
Проверим теперь концы интервала:
- необходимое условие сходимости не выполнено. Ряд расходится.
Ряд расходится
Ответ:
Похожие вопросы