Предмет: Алгебра,
автор: milleralinagang
сделайте пж ,покозательные уравнение
Приложения:
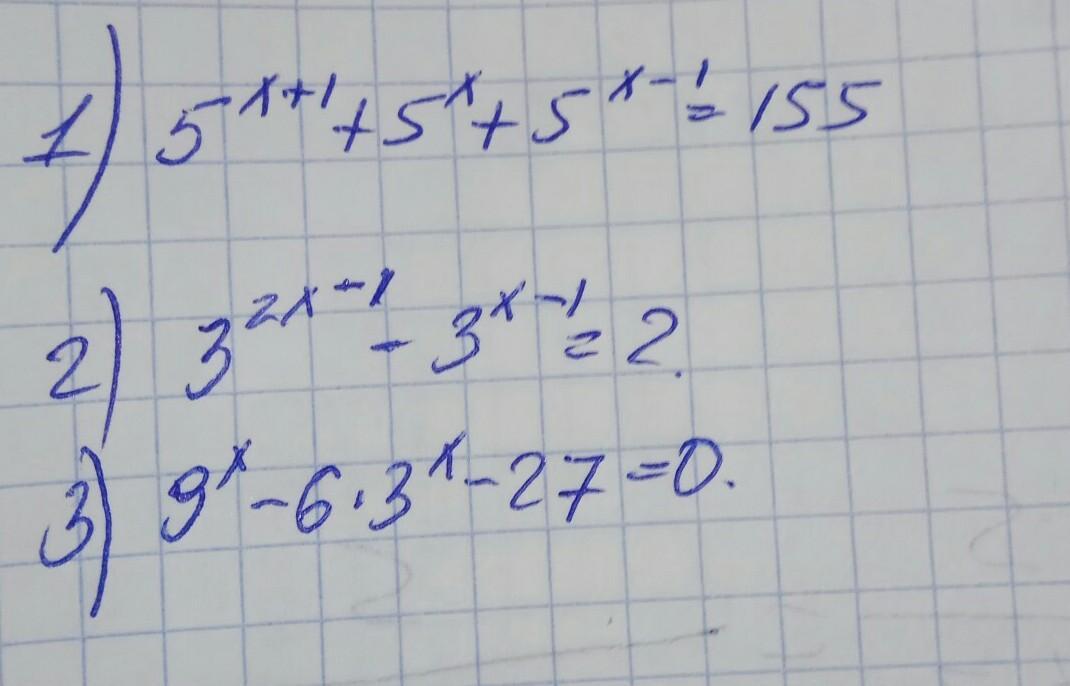
Ответы
Автор ответа:
1
Первое уравнение
Вынесём множитель за скобки:
Второе уравнение
Сделаем замену :
Вернёмся к исходной переменной:
а)
б)
Показательная функция принимает только положительные значения, поэтому последнее уравнение не имеет решений.
Ответ:
Третье уравнение
Сделаем замену :
Вернёмся к исходной переменной:
а)
б)
Показательная функция принимает только положительные значения, поэтому последнее уравнение не имеет решений.
Ответ: .
milleralinagang:
спасибо большое
только мы log не изучаем
Ну тогда запишите просто 5^x=25, 5^x=5^2, x=2 — это в первом
Вто втором 3^x=3^1, x=1
хорошо,спасибо большое)
В третьем 3^x=9, 3^x=3^2, x=2
Похожие вопросы
Предмет: Математика,
автор: Outsider02
Предмет: Русский язык,
автор: ygawydgyawdy
Предмет: Информатика,
автор: maratayupov0
Предмет: Математика,
автор: lomtic
Предмет: Математика,
автор: kam42