Предмет: Алгебра,
автор: 2004maxim
2приклади
Поможіть
Записати не можу тому дивіться на фото.
Приложения:
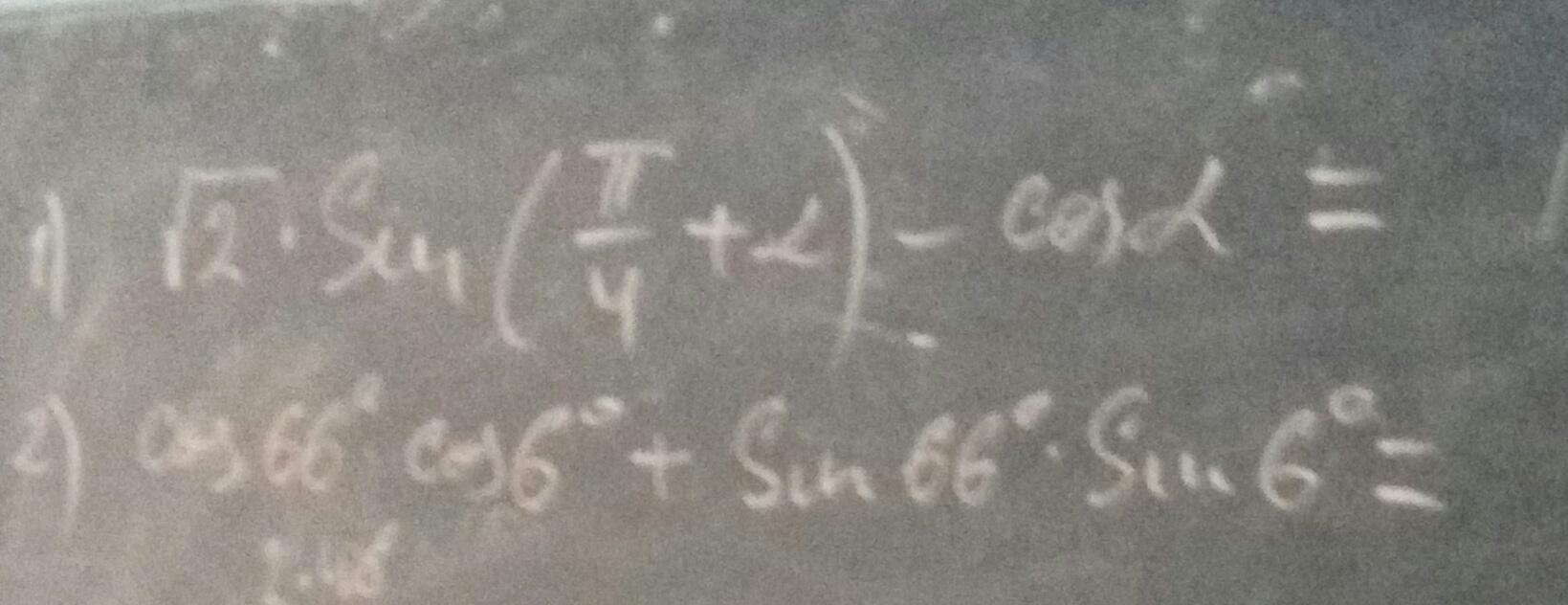
Ответы
Автор ответа:
1
Якщо що-небудь буде незрозуміло — запитуйте. Якщо моя відповідь виявилася корисною, натискайте «спасибі» й відмічайте її як «найкращу відповідь».
Відповідь:
Відповідь:
Похожие вопросы
Предмет: Литература,
автор: Matroskin777
Предмет: Алгебра,
автор: yfoycoyci
Предмет: Алгебра,
автор: znanyazna
Предмет: Химия,
автор: настя1420027
Предмет: Геометрия,
автор: Akbarzodamasha23