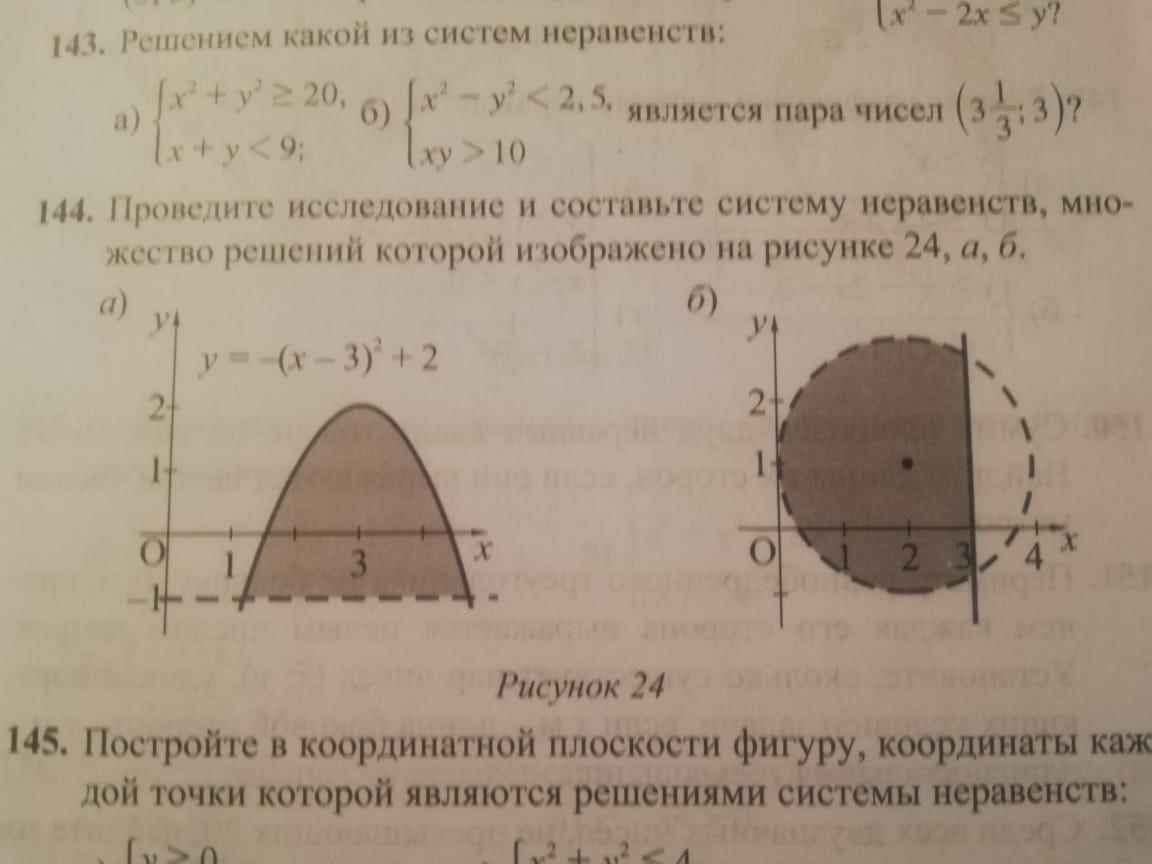
проведите исследование и составьте систему неравенств, множество решений которой изображено на рисунке 24,а,б.
Ответы
Объяснение:
Если нужна система неравенств, то пишем уравнения.
Задача а)
1) у = -(х - 3)² + 2 - парабола
2) y ≥ - 1 - прямая
Находим границы Х решив уравнение.
3) - (х - 3)² + 2 = -1
4) -(х² - 6*х +9) + 3 = 0
5) -х² + 6*х - 6 = 0
Решаем квадратное уравнение.
D=12, √12 = 2√3.
Корни ... х1 = 3-√3 ≈ 1,27 и х2 = 3+√3 ≈ 4,73 -
3 -√3 ≤ Х ≤ 3 +√3 ответ
Задача б)
Пересечение окружности и прямой.
Уравнение окружности
1) (x - 2)² + (x - 1)² = 2² ≤ 4 - внутри окружности
2) 0 ≤ x ≤ 3 - левее прямой
Объяснение:
- Парабола ветвями вниз, смещена на (3; 2)
1) D(y) = R
2) E(y) = (-∞; 2]
3) неприрывная, не четная
4) Нули: y = 0, при x = -√2 + 3; x = √2 + 3
5) y > 0 при x ∈ (-√2+3; √2+3);
y < 0 при x ∈ (-∞; -√2+3) U (√2+3; +∞)
6) Возрастает на промежутке x ∈ (-∞; 3]
Убывает на промежутке x ∈ [3; +∞)
7) Ymax = 2
Система:
y < -(x - 3)² + 2
y > -1
- не является графиком (уравнение окружности)
Система:
(x - 2)² + (y - 1)² < 4
x < 3