Предмет: Геометрия,
автор: tereziyavanastreya
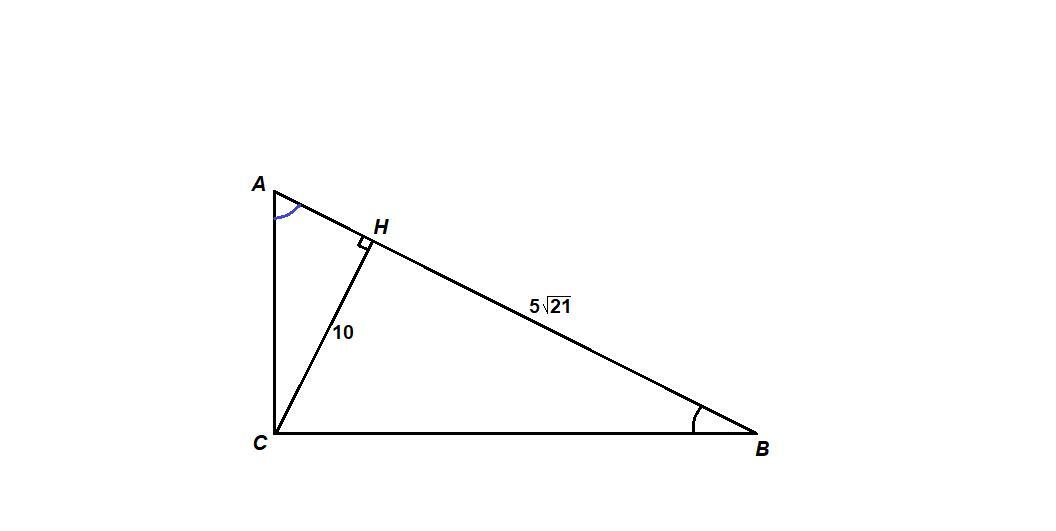
В треугольнике ABC угол C равен 90°, высота CH равна 10, BH = 5√21. Найдите cosA.
Ответы
Автор ответа:
0
Ответ:
cosA = 0,4
Объяснение:
ΔBCH: ∠BHC = 90°, по теореме Пифагора
BC = √(CH² + BH²) = √(100 + 25 · 21) = √(100 + 525) = √625 = 25
∠A + ∠B = 90° по свойству острых углов прямоугольного треугольника.
∠А = 90° - ∠В
Приложения:
Похожие вопросы
Предмет: Обществознание,
автор: permaykov76
Предмет: Математика,
автор: vb532226
Предмет: Алгебра,
автор: tem4ik2221
Предмет: Математика,
автор: мими143
Предмет: Математика,
автор: смат3