Как это решить? 1.В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 и 12 см. Найти катеты треугольника.
2.Найти диагональ и боковую сторону равнобедренной трапеции с основаниями 10 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции.
???
Ответы
Ответ:
Задача 1:
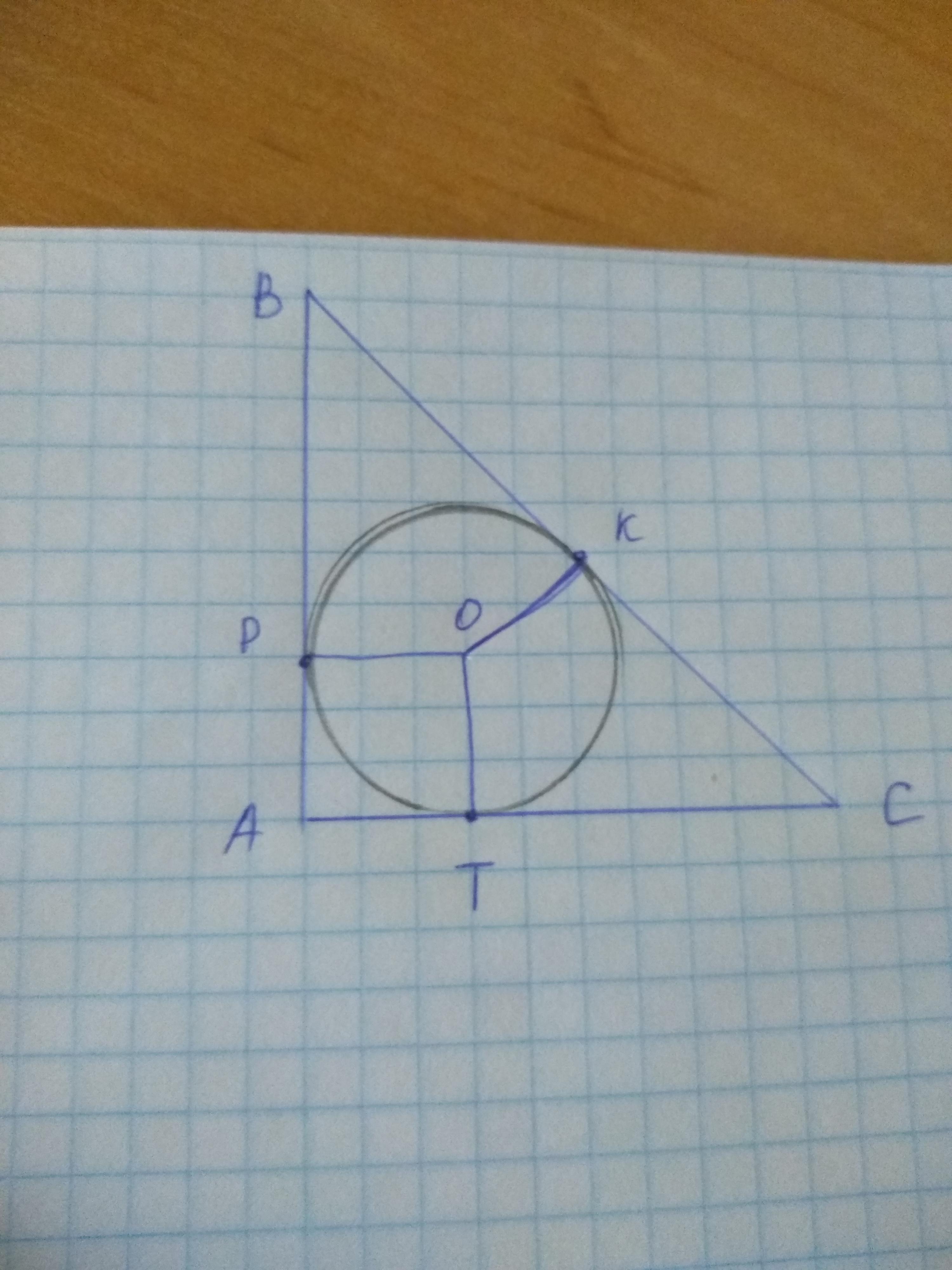
По рисунку видно, что ВС - гипотенуза.
ВК = 12см, КС = 5 см, ОК = ОТ = ОР = радиусы.
Свойства описанного прямоугольного треугольника твердят, что (по рисунку)
а) РО = ОТ = РА = АТ , Получается квадрат АРОТ у котого все стороны равны;
б) РВ = ВК = 12 см
с) КС = ТС = 5 см
Пусть АР = АТ = х см, тогда АВ = 12 + х, АС = х + 5, ВС = 12 + 5 = 17 см
Используем теорему Пифагора:
ВС² = АВ² + АС²
17² = (12 + х)² + (х + 5)²
289 = 144 + 24х + х² + х² + 10х + 25
2х² + 34х - 120 = 0 скоротим на 2
х² + 17х - 60 = 0
ищем дискриминантом
Д = 289 + 240 = 529 = 23²
х1 = 3
х2 = -20 - не удовлетворяет.
АВ = 12 + 3 =15см
АС = 3 + 5 = 8см
Ответ: 15см, 8 см.
Задача 2:
Пусть АД - диаметр окружности, описанной около равнобелренной трапеции АБСД с основаниями АД = 12см и БС= 10 см. СН - перпендикуляр, опущенный из вершины С на основание АД. Тогда:
АН=(АД+БС)/2= (12+10)/2=11 см
ДН=(АБ-БС)/2=(12-10)/2= 1 см
Точка С лежит на окружности с диаметром АД, значит угол АСД=90 градусов, поэтому СН высота прямоугольного треугольника АСД, проведенная из вершины прямого угла. Следовательно:
СД=ДН*АД=1*12=12см
АС=АН*АД=11*12=132 см
Пошаговое объяснение: