Question

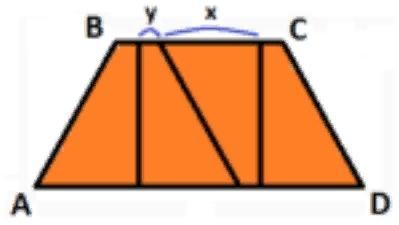
Четырёхугольник АВСД имеет две параллельные стороны ВС и АД , причем АВ=2, ВС=2 , СД=2 и АД=4 . Данный четырехугольник разбили на 4 равных четырехугольника. В результате верхняя сторона разделилась на четыре отрезка. Найдите отношение длины х большего отрезка к длине у меньшего.

Answer 1

Ответ:

4

Пошаговое объяснение:

Четыре мелких четырехугольника равны, поэтому:

Длина BC состоит из трех Y и одного X, и равна 2.

Длина AD состоит из трех X и одного Y, и равна 4.

Запишем уравнения:

3*Y + X = 2

Y + 3*X = 4

Из второго уравнения Y = 4 - 3*X

Подставим Y в первое уравнение:

3*(4 - 3X) + X = 2

12 -9X + X = 2

-8X = -10

X=1,25

Подставим X во второе уравнение.

Y + 3*1,25 = 4

Y = 4 - 3,75

Y = 0,25

Отношение X к Y равно 1,25 / 0,25 = 4.