Предмет: Математика,
автор: Argji
Вычислить двойной интеграл
Приложения:
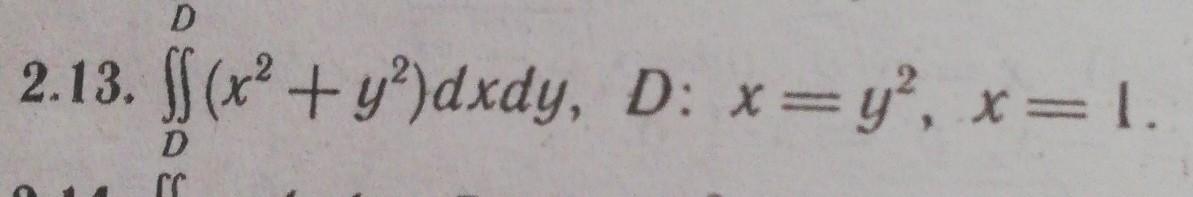
Ответы
Автор ответа:
1
Ответ:
32/63
Пошаговое объяснение:
Будем интегрировать по x, меняясь от 0 до 1, по y будем интегрировать от 0 до √x
Тогда:
Похожие вопросы
Предмет: Русский язык,
автор: killkillnasyrov
Предмет: Русский язык,
автор: neznakomaya78
Предмет: Физика,
автор: jjeosow
Предмет: Математика,
автор: 35354033