Question

Какой угол образует с осью абцисс касательная к параболе f(x)=x^2-3x+5, проведённая в точке M0 (2;3)​

Answer 1

Производная функции: $f'(x)=(x^2-3x+5)'=2x-3$.

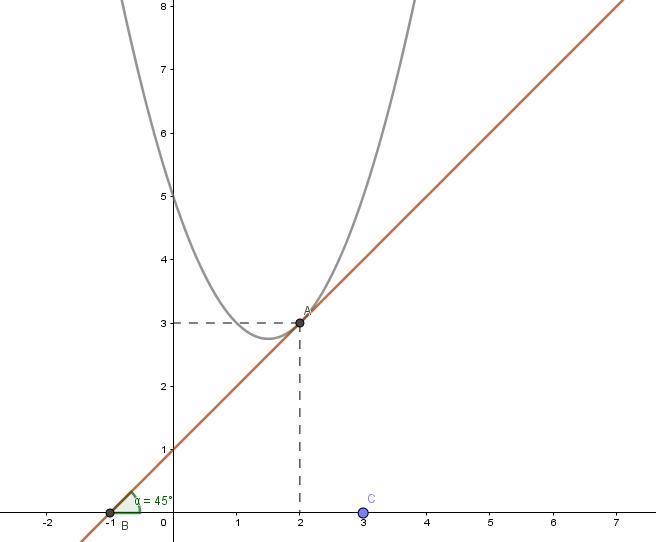
Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке или равна тангенсу угла наклона касательной.

В нашем случае, абсцисса точки касания x₀ = 2

$f'(x_0)=k={\rm tg}\, \alpha\\ \\ 2\cdot 2-3={\rm tg}\, \alpha\\ \\ {\rm tg}\, \alpha=1\\ \\ \alpha = 45^\circ$

Ответ: 45°.

Answer 2

угловой коэффициент касательной к графику функции у= f(x)=x²-3x+5, в точке М с абсциссой х₀=2, равен значению производной функции в точке касания. Производная f'(x)=(x²-3x+5)'=2х-3

f'(2)=2²-3=4-3=1

к=1, к=tgα, где α-угол между касательной и положительным направлением оси абсцисс.

График во вложении. α=45°