Предмет: Математика,
автор: FID1371
cos(x) + 2cos(2x+π/6)=√3cos(2x)
Ответы
Автор ответа:
3
Ответ:
решение представлено на фото
Приложения:
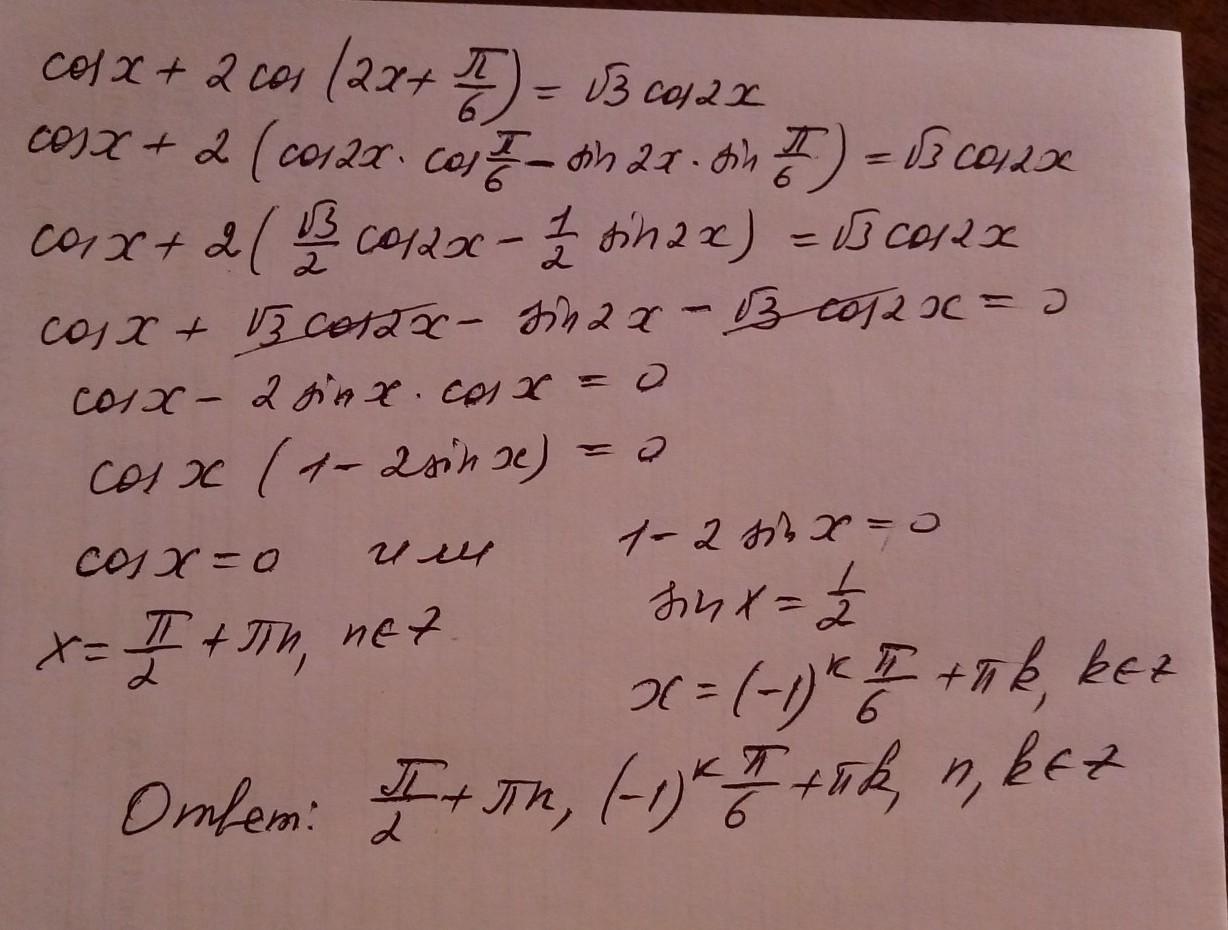
Автор ответа:
2
Произведение равно нулю в том случае, когда хотя бы один из множителей обращается к нулю.
Похожие вопросы
Предмет: Математика,
автор: alyonamkrft
Предмет: Алгебра,
автор: danyahomenko209
Предмет: Физика,
автор: dedinsai9
Предмет: Математика,
автор: ntemeshev
Предмет: Алгебра,
автор: nastenayurkova