Предмет: Геометрия,
автор: aznaur038
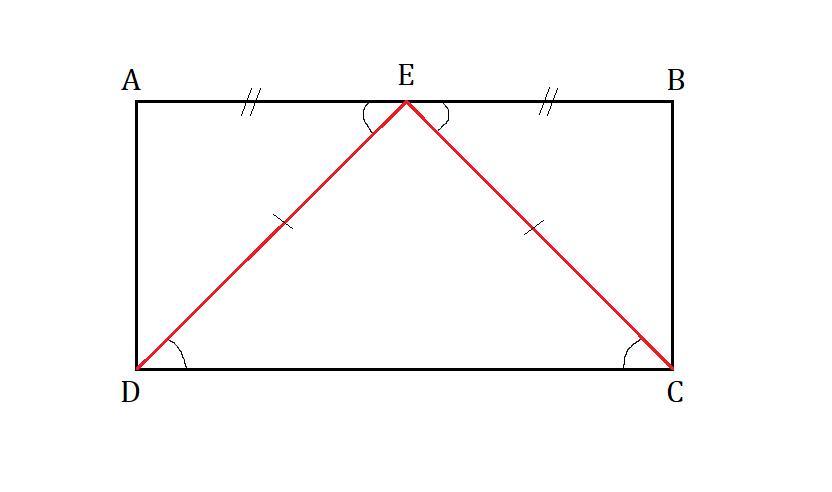
В параллелограмме ABCD точка E - середина стороны AB. Известно, что EC = ED. Докажите , что данный параллелограмм - прямоугольник
Ответы
Автор ответа:
1
Ответ:
Что и требовалось доказать!
Объяснение:
Так как - равнобедренный ⇒
В параллелограмме противоположные стороны параллельны.
При пересечении двух параллельных секущей, накрест лежащие углы равны.
Но так как , по свойству ⇒
Так как - середина
⇒
по условию.
⇒ по 1 признаку равенства треугольников.
⇒
В параллелограмме сумма односторонних углов равна .
Т.к. .
В параллелограмме сумма односторонних углов равна .
⇒
⇒
Параллелограмм, у которого все углы прямые - прямоугольник.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: nikitosua77777
Предмет: Английский язык,
автор: dogarci09
Предмет: Математика,
автор: vikakravch10
Предмет: Физика,
автор: master62
Предмет: Информатика,
автор: настя4584