Предмет: Алгебра,
автор: nik04ta01
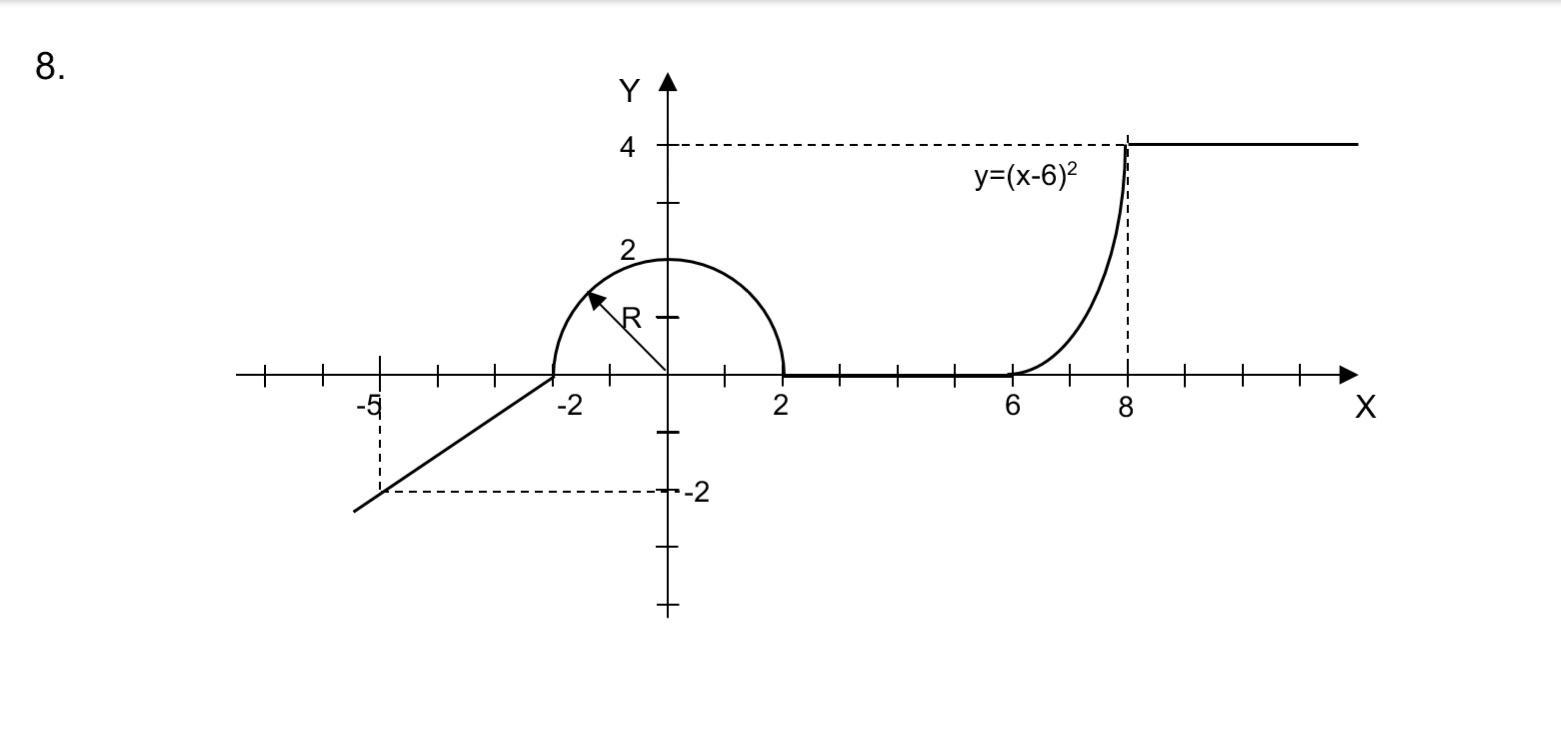
Помогите пожалуйста составить все эти уравнения по картинке и решить их.
Ps я их составил, но какие числа в них подставлять я без понятия. Заранее спасибо
y=kx +b
x²+y²=R²
y=(x-6)²
Приложения:
Ответы
Автор ответа:
1
Уравнение прямой, проходящей через точки ( -5,-2) и (-2,0) имеет вид y=kx+b:
Уравнение окружности с центром в точке и радиусом, равным R, имеет вид:
.
Тогда окружность на рисунке имеет вид:
Если перед корнем берём знак (+), то получаем уравнение верхней полуокружности (y≥0) , а если берём знак (-), то получаем уравнение нижней полуокружности (у≤0) .
Уравнение прямых, проходящих параллельно оси ОХ через точку с координатами (a,b) , имеет вид: у=b .
Аналитически заданная на графике функция имеет вид:
Приложения:

Похожие вопросы
Предмет: Физика,
автор: Аноним
Предмет: Алгебра,
автор: 0999549556a
Предмет: Биология,
автор: tanasolovej036
Предмет: Математика,
автор: Wafiqa30
Предмет: Математика,
автор: ксюха176