Предмет: Алгебра,
автор: Nik00789
Пожалуйста решите неравенство
Приложения:
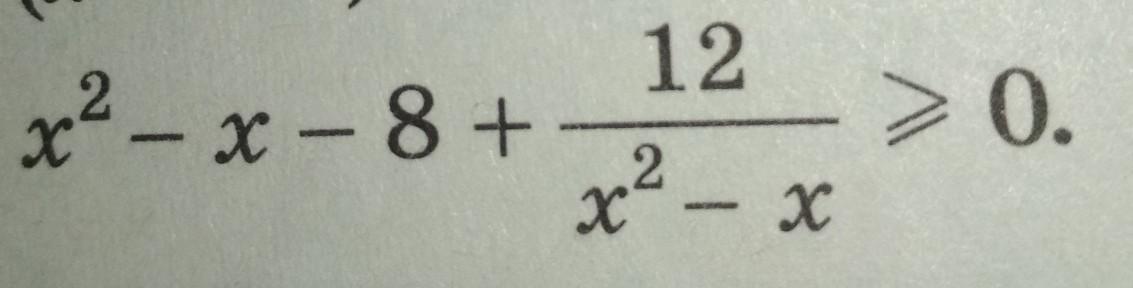
Ответы
Автор ответа:
0
Рассмотрим функцию . Найдем ее область определения: функция существует когда знаменатель дроби не обращается к нулю
Приравниваем функцию к нулю, т.е. f(x) = 0
Решаем как квадратное уравнение относительно . По теореме Виета
__+___[-2]__-___[-1]__+__(0)__-__(1)__+__[2]___-___[3]__+____
Ответ:
Автор ответа:
0
Ответ и пояснения во вложении
Приложения:

Похожие вопросы
Предмет: Другие предметы,
автор: ivamek
Предмет: Математика,
автор: darbaybirzhan
Предмет: Геометрия,
автор: ytfirehack
Предмет: География,
автор: лера1493