Question

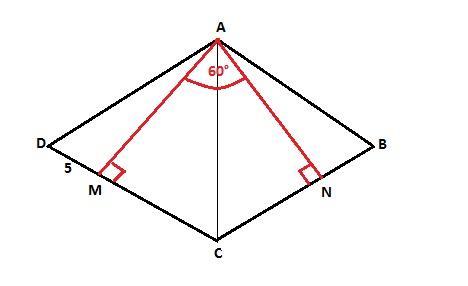
7. (36) В ромбе ABCD с вершины тупого угла А проведено высоты AMи ANK
сторонам DC и BC соответственно. Найти периметр ромба, если
угол MAN = 60°, DM = 5 дм.​

Answer 1

Ответ:

Pabcd = 40 дм.

Объяснение:

Прямоугольные треугольники DAM и BAN равны по гипотенузе и острому углу (гипотенузы DA и АВ -  стороны ромба, ∠D = ∠B как противоположные углы ромба). Следовательно, ∠DAM = ∠BAN, а так как диагональ АС ромба делит ∠DAB пополам (свойство), то ∠MAC = <NAC = 30°. Тогда в прямоугольных треугольниках MAC и NAC ∠АСМ = ∠ACN = 60° (по сумме острых углов прямоугольного треугольника). Тогда угол ∠С ромба равен 120°, а ∠D = 60° (по сумме углов ромба, прилегающих к одной стороне).

В прямоугольном треугольнике DAM ∠ADM = 60°, ∠DAM=30°.

Против угла 30° лежит катет DM = 5 дм. Тогда гипотенуза DA (сторона ромба) равна 10 дм, а периметр ромба равен

10·4 = 40 дм.