Построить линии по уравнениям
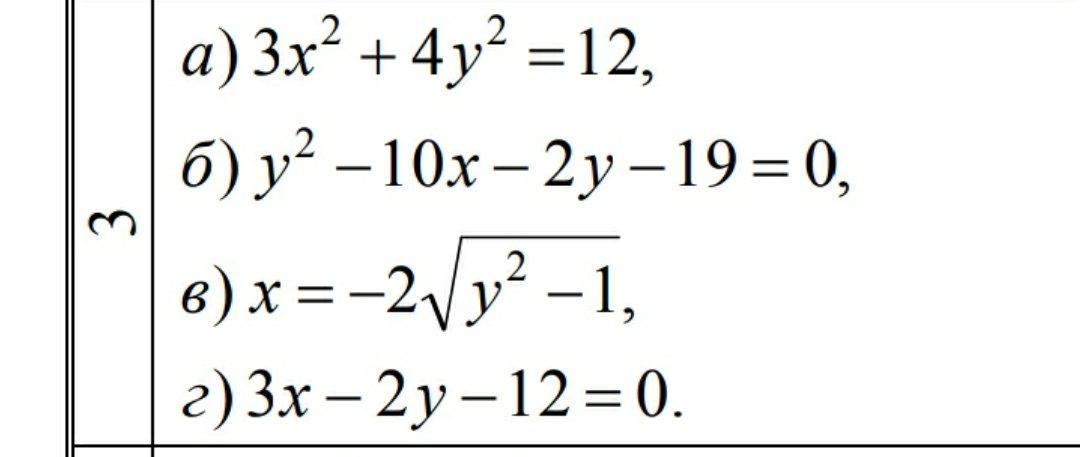
Ответы
a) Если разделить обе части уравнения на 12, то получим каноническое уравнение эллипса:
Параметры: а = +-2, в = +-√3.
Это координаты по осям Ох и Оу.
Выразим уравнение относительно у:
у = +-√((12 - 3х²)/4).
Получим ещё 4 точки для построения, если х = +-1, то у = +-1,5.
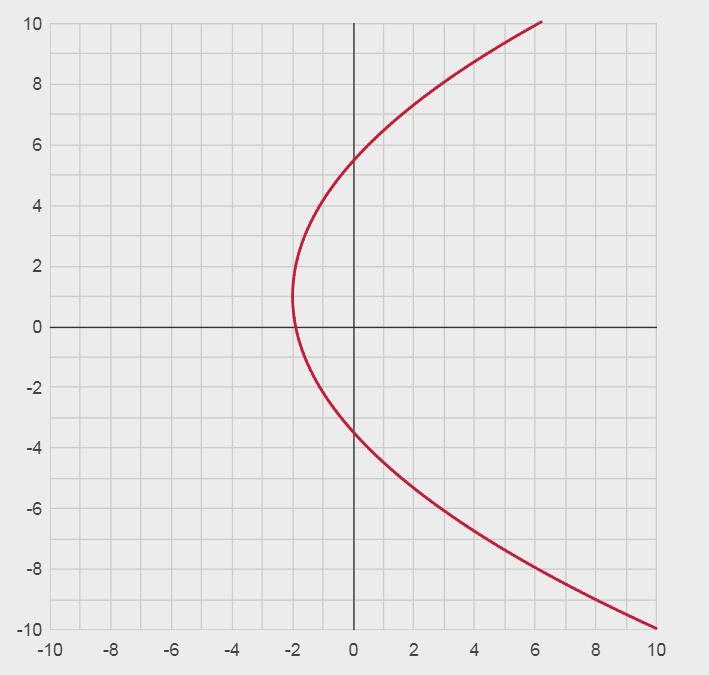
б) Дано уравнение y² - 10x - 2y - 19 = 0.
Выделяем полные квадраты:
(y²-2·1y + 1) -1 = (y-1)²-1 .
Преобразуем исходное уравнение:
(y-1)² = 10x + 20
Получили уравнение параболы:
(y - y0)² = 2p(x - x0)
(y-1)² = 2·5(x - (-2))
Ветви параболы направлены вправо, вершина расположена в точке (x0, y0), т.е. в точке (-2;1)
Параметр p = 5
Координаты фокуса: F = ((x0 - (p/2);yo)= (-2 + (5/2) = 0,5; 1) = (0,5; 1).
Уравнение директрисы: x = x0 - (p/2)
x = -2 - (5/2) = -9/2.
График приведен во вложении.
в) Это симметричный график в 3 и 4 четвертях.
Строится по точкам при y ≥ 1:
y = 1 2 3 4 5
x = 0 -3,46 -5,66 -7,75 -9,8.
Для отрицательных значений "у" значения "х" те же самые.
г) Это уравнение прямой, строится по двум точкам.
Уравнение относительно у: у = (-3/2)х + 6.
х = 0, у = 6,
х = 4, у = 0