Question

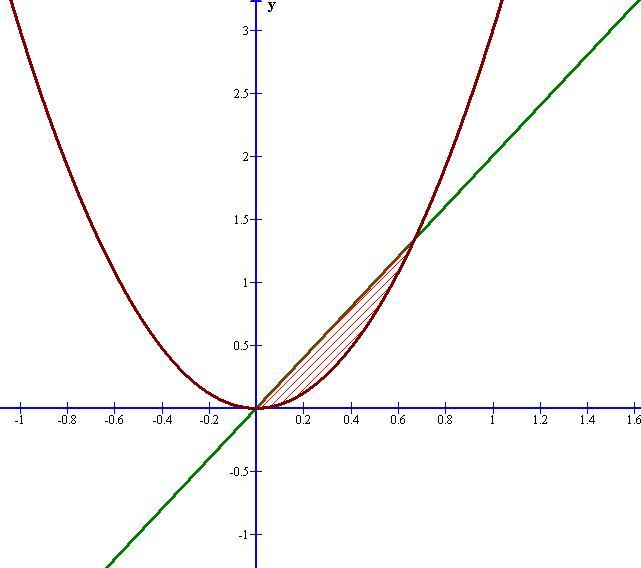
Найдите площадь фигуры, ограниченной графиками заданных функций.

y=3x^2, y=2x.

Answer 1

$y=3x^2$ - парабола, ветви которой направлены вверх.

$y=2x$ - прямая, проходящая через начало координат.

Приравниваем функции и найдем ограниченные линии

$3x^2=2x\\ 3x^2-2x=0\\ x(3x-2)=0\\ x_1=0\\ x_2=\frac{2}{3}$

Площадь фигуры:

$S=\displaystyle \int\limits^{\frac{2}{3}}_0\left(2x-3x^2\right)dx=\left(x^2-x^3\right)\big|^{\frac{2}{3}}_0=\bigg(\frac{2}{3}\bigg)^2\cdot \bigg(1-\frac{2}{3}\bigg)=\frac{4}{9}\cdot\frac{1}{3}=\frac{4}{27}$

Ответ: 4/27 кв. ед.