Предмет: Алгебра,
автор: elvinamamedova2019
Решить предел , без правила Лопиталя !!!
Приложения:
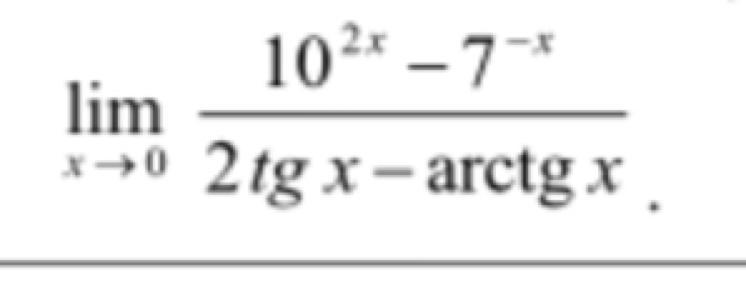
Ответы
Автор ответа:
1
Здесь будут использоваться замечательные пределы
Ответ: ln700.
1574577:
Пожалуйста помогите мне с геометрией.
Похожие вопросы
Предмет: Английский язык,
автор: aesthetikgirl2021
Предмет: Литература,
автор: Lovekakashki
Предмет: Другие предметы,
автор: walushka1964
Предмет: Литература,
автор: Айзада76668
Предмет: Литература,
автор: ramazanovvaler