Question

30 баллов!!!!!!!!!!!!
Постройте график дробно-линейной функции у=3х-7/х+1

Answer 1

ДАНО: y =(3*x-7)/(x+1)

Объяснение:

1) Область определения функции.

Деление  в знаменателе на 0 - не допустимо.

х +1  ≠ 0 и х ≠ -1

ООФ - D(y)∈(-∞;-1)∪(-1;+∞)

2) Вертикальная асимптота - Х= -1. Разрыв II-го рода.

3) Пересечение с осью ОУ при Х=0.

У(0) = -7

4) Пересечение с осью ОХ - У(х)=0 - нуль функции.

3*х - 7 = 0

Х = 7/3 = 2,(3) -  нуль функции.

5) Проверка на чётность.

y(-x) = (-3*x-7)/(-x-1) - функция общего вида. Ни чётная ни нечётная.

6) Экстремумы функции - по первой производной.

$y'(x) = \frac{3}{x+1}-\frac{3*x-7}{(x+1)^2}=\frac{10}{(x+1)^2}$

Корней нет. Экстремумы в точке разрыва - Х = -1.

7) Монотонность функции.

Возрастает - Х∈(-∞;-1)∪(-1;+∞)

8) Выпуклость по второй производной.

y"(x) = - 20/(x+1)³ = 0.

Корней нет - точка перегиба в точке разрыва при Х = -1.

9) Вогнутая - У"(x)≥0  при Х∈(-∞;-1)

Выпуклая - У"(x)<0 при Х∈(-1;+∞)

10) Горизонтальная асимптота - прямая - y = k*x+b.

$k= \lim_{x \to \infty} \frac{3*x-7}{(x^2+x)}=0\\   b= \lim_{x \to \infty}\frac{3x-7}{x+1}-0*x=3$

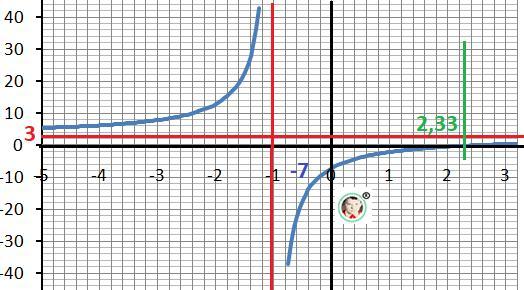
График на рисунке в приложении.

КРАСОТА.