Question

15 БАЛЛОВ. на отрезок длиной 10см ставятся две точки. найти вероятность того, что из трёх получившихся частей можно составить треугольник. тема: геометрическое определение вероятности. решать, используя омегу и тд.​

Answer 1

Пусть x, y и 10 - x - y  — части отрезка. Тогда имеем ограничения

$0\leq x\leq 10\\ 0\leq y\leq 10$

$x+y\leq 10$

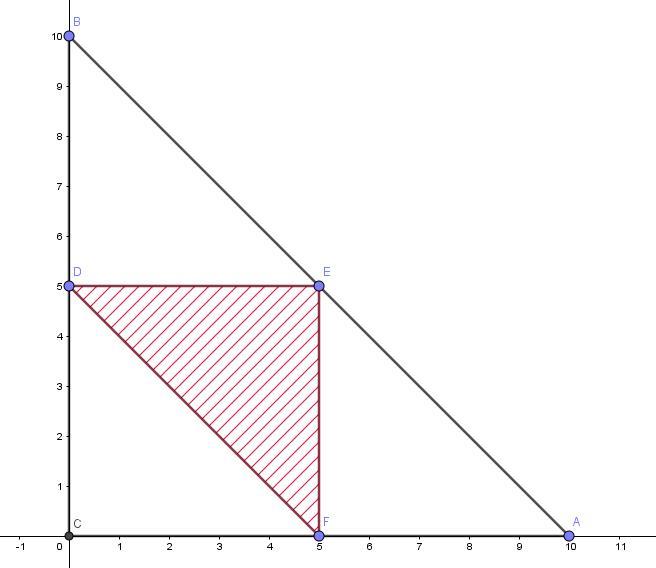
На рисунку у нас треугольник, ограниченный осями координат и прямой $x+y\leq 10$

По неравенству треугольника: сумма длин двух сторон не превышает третью сторону.

$10-x-y\leq x+y~~~\Rightarrow~~~~ \boxed{x+y\geq5}$

$x\leq 10-x-y+y~~~~\Rightarrow~~~ \boxed{x\leq 5}\\ \\ y\leq10-x-y+x~~~\Rightarrow~~~ \boxed{y\leq 5}$

Количество всевозможных исходов: площадь тр-ка ABC

$n(\Omega)=\dfrac{10\cdot10}{2}=50$

Площадь заштрихованного треугольника DEF:

$S_{FED}=\dfrac{FE\cdot DE}{2}=\dfrac{5\cdot 5}{2}=\dfrac{25}{2}$ кв.ед.

$n(A)=\dfrac{25}{2}$

Искомая вероятность по формуле геометрической вероятности

$P(A)=\dfrac{n(A)}{n(\Omega)}=\dfrac{25/2}{50}=\dfrac{1}{4}$

Ответ: 1/4.