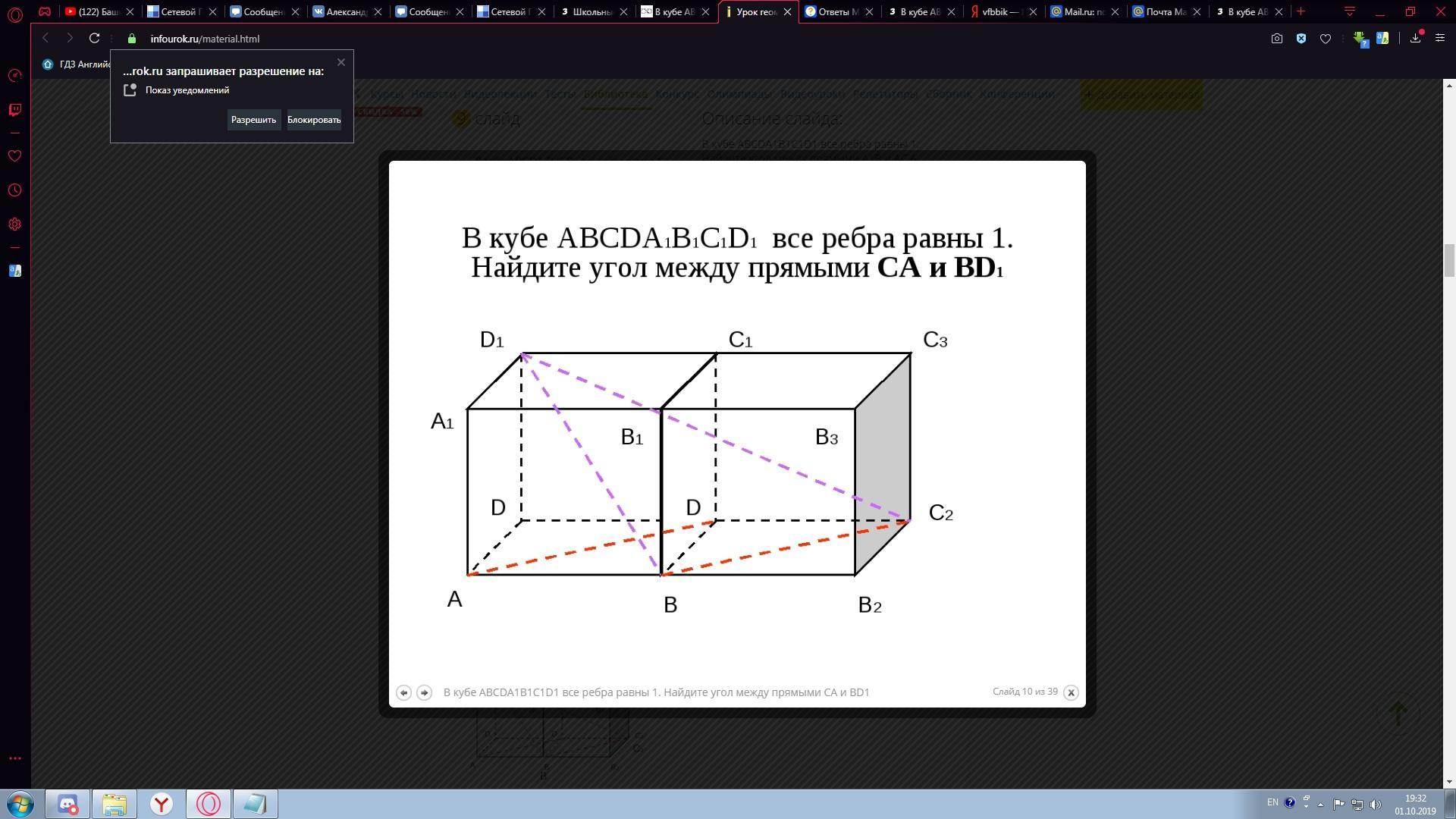
В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите угол между прямыми CА и BD1
Ответы
Ответ:
ВD1 - диагональ куба, DA1 - диагональ грани АА1D1D.
BD1 и DA1 - скрещивающиеся прямые.
Диагональ грани можно найти по теореме Пифагора:
DA1=√(AD²+AA1²)=√(1+1)=√2.
Диагональ куба можно найти , применив два раза теорему Пифагора:
ВD=√(AD²+AB²)=√2 , BD1=√(BD²+²DD1²)=√(2+1)=√3 .
Теперь проведём прямую D1A2║DA1 в плоскости AA1D. Мы как бы достроим пл. AA1D1D до пл. AA2D2D. Получили, что плоск. AA2D2D - прямоугольник, причём D1A2=DA1=√2.
Теперь можем соединить точки В и А2, т.к. они лежат в одной плоскости АВА2.
Рассмотрим ΔВА2D1. Угол BD1A2 будет искомым углом, т.к. угол между скрещивающимися прямыми можно найти как угол между прямыми, параллельными заданным скрещивающимся прямым.
Найдём ВА2 из ΔАВА2: ∠ВАА2=90° , АВ=1, А1А2=1+1=2 ( по построению).
ВА2=√(АВ²+АА2²)=√(1+4)=√5 .
Применим теорему косинусов для ΔВА2D1:
BA2²=D1A2²+BD1²-2·D1A2·BD1·cos∠BD1A2
5=2+3-2·√2·√3·cos∠BD1A2 ⇒ cos∠BD1A2=0 ⇒ ∠BD1A2=90°
Подробнее - на Znanija.com - https://znanija.com/task/29341365#readmore
Объяснение:
Может быть не правильно( не проверял