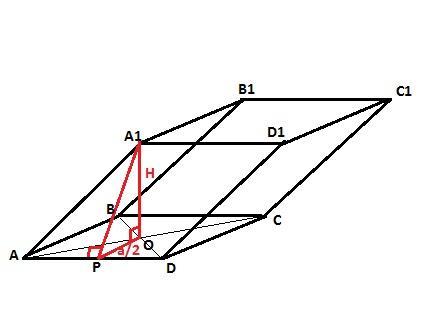
Основа похилого паралелепіпеда квадрат із стороною (а) одна з вершин основи проектується центр цьго квадрата .Висота паралелепіпеда Н. Знайдіть бічну поверхню паралелепіпеда .
Ответы
Ответ:
Sб = 2а·√(H²- a²) ед².
Объяснение:
Площадь боковой поверхности параллелепипеда - это сумма площадей четырех боковых граней этого параллелепипеда. Так как в основании данного нам параллелепипеда лежит квадрат, то площади боковых граней (равных параллелограммов) одинаковы. Они равны произведению стороны основания на высоту грани. Так как высота наклонного параллелепипеда равна перпендикуляру, опущенному из вершины на плоскость основания, а этот перпендикуляр в нашем случае опущен в центр квадрата, то высоту грани найдем по Пифагору из прямоугольного треугольника, образованного высотой параллелепипеда, половиной стороны основания (катеты) и высотой боковой грани (гипотенуза).
h = √(H²- a²/4) = √(H²- a²)/2 ед. Тогда площадь одной грани равна
Sгр = а·√(H²- a²)/2 ед². Площадь боковой поверхности (4 граней):
Sб = 2а·√(H²- a²) ед².