Предмет: Алгебра,
автор: Таволга
Решите неравенство
В ответе получается (3;4);(4;5]
У меня не сошлось с ответом
Приложения:
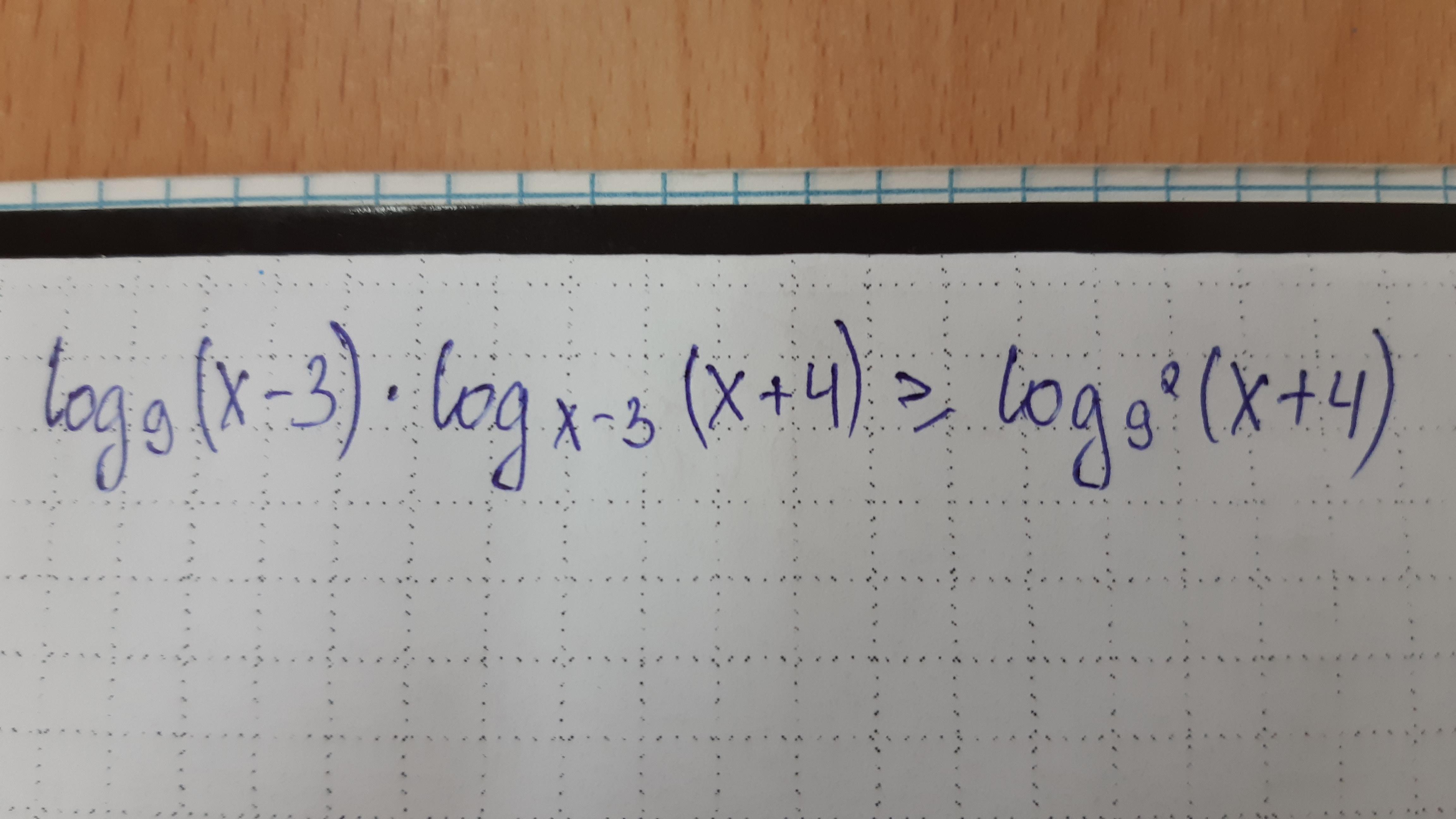
Simba2017:
(3;5]
не пойму почему 4 исключена
поняла , из-за одз,
да ответ верный
что означает ваше "да ладно?"
смотрите свойства логарифмов-ответ забивать не стану.....
девять в квадрате или сам логарифм в квадрате?
Да, логарифм в квадрате, да ответ такой же
Ответ должен быть (4;5]
Ой, (3;4)
Ответы
Автор ответа:
1
Рассмотрим функцию . Ее область определения:
Решим уравнение f(x) = 0
Произведение равно нулю в том случае, когда хотя бы один из множителей обращается к нулю
(3)____+__(4)___+____[5]______-_______>
Ответ: x ∈ (3;4)∪(4;5]
Автор ответа:
1
Ответ и решение во вложении
Приложения:

Похожие вопросы
Предмет: Геометрия,
автор: Аноним
Предмет: Геометрия,
автор: FaerVator
Предмет: Обществознание,
автор: xxxmark21zzz
Предмет: Физика,
автор: feechka666
Предмет: Математика,
автор: crazyfqce