Предмет: Математика,
автор: Hdjdjfhcch
Под буквой
а) доказать что числа являются не взаимно простые.
б) доказать что числа являются взаимно простые.
Приложения:
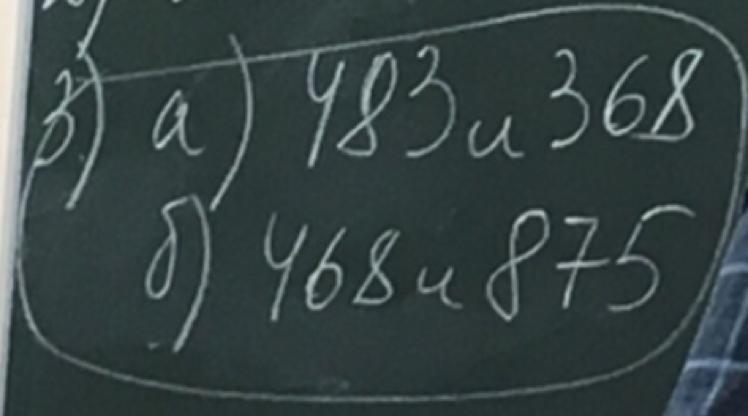
Ответы
Автор ответа:
5
Ответ:
Пошаговое объяснение:
а) 483 = 3 * 7 * 23 * 1
368 = 2 * 2 * 2 * 2 * 23 * 1
НОД = 23 * 1 = 23
НОД не равен = 1, значит не взаимно простые
б) 468 = 2 * 2 * 3 * 3 * 13 * 1
875 = 5 * 5 * 5 * 7 * 1
НОД = 1 * 1 = 1
НОД = 1 значит взаимно простые
Автор ответа:
2
Ответ:
Пошаговое объяснение:
НОД (483 и 368) =23 не явл. взаимно простыми числами
разложим на множители:
483=1*3*7*23
368=1*2*2*2*2*23
НОД (468 и 875)=1
468=1*2*2*3*3*13
875=1*5*5*5*7
являются взаимно простыми числами, т.к. имеют один общий делитель и он = 1.
Похожие вопросы
Предмет: Алгебра,
автор: vrusyt22
Предмет: Алгебра,
автор: ghoulsgg777
Предмет: Математика,
автор: angelinangy2010
Предмет: История,
автор: Dzudo1
Предмет: Математика,
автор: май30