Предмет: Алгебра,
автор: danielsitravelu
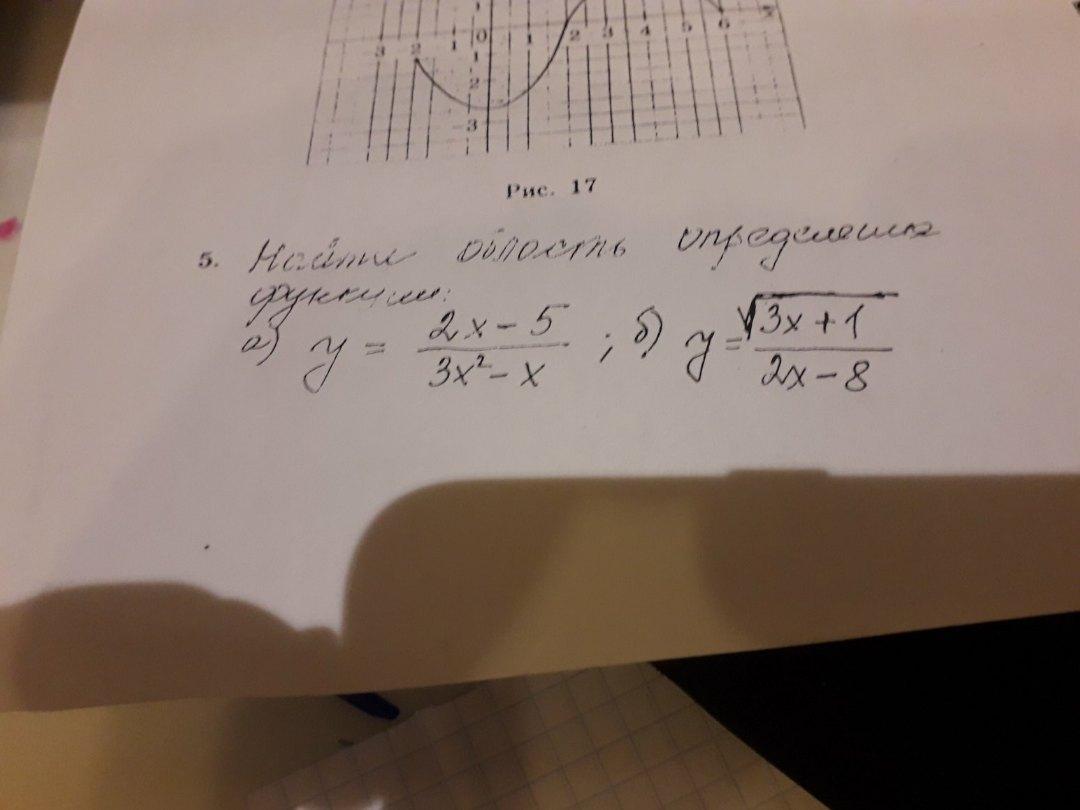
Помогите с задачей по алгебре!!! Нужно найти область определения функции.
a) y=2x-53x^2-x/3x^2-x
б) y=√3x+1/2x-8
Приложения:
Ответы
Автор ответа:
1
Знаменатель дроби не должен равняться нулю, так как на ноль делить нельзя.
3x² - x ≠ 0
x(3x - 1) ≠ 0
Во-первых, выражение стоящее под корнем чётной степени должно быть неотрицательным, то есть ≥ 0 . Во- вторых, знаменатель дроби не должен равняться нулю. Обязательно должны выполняться оба эти условия .
Похожие вопросы
Предмет: Биология,
автор: katalanovenko7
Предмет: Алгебра,
автор: vadimmacitov65700
Предмет: Математика,
автор: SeeUSyn
Предмет: Биология,
автор: aidar123E
Предмет: Алгебра,
автор: alina05112003as