Предмет: Геометрия,
автор: noname123426
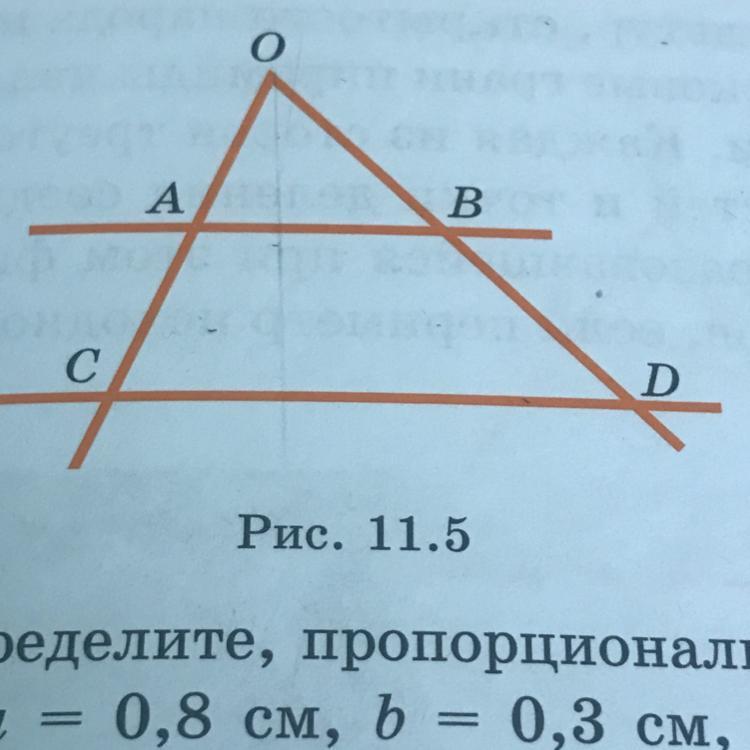
Стороны угла с вершиной О пересечены двумя параллельными прямыми в точках А,С и В,D соответственно ( рис. 11.5 ).
Найдите ОС, если ОВ=BD=5 и ОА=4.
Помогите плиз
Приложения:
Ответы
Автор ответа:
221
Ответ:
8 ед.
Объяснение:
Воспользуемся данным рисунком
AB║CD по условию.
ΔOAB подобен Δ OCD по двум углам
∠OAB=∠OCD как соответственные, образванные AB║CD и
секущей ОС, ∠О - общий.
Тогда у подобных треугольников соответствующие стороны пропорциональны.
ед.
Похожие вопросы
Предмет: Математика,
автор: Geenii195
Предмет: Математика,
автор: Rayna3226
Предмет: Алгебра,
автор: kurinnaykatay1388
Предмет: Биология,
автор: Амалия3333
Предмет: Алгебра,
автор: logon03