Предмет: Алгебра, автор: ParkKarina

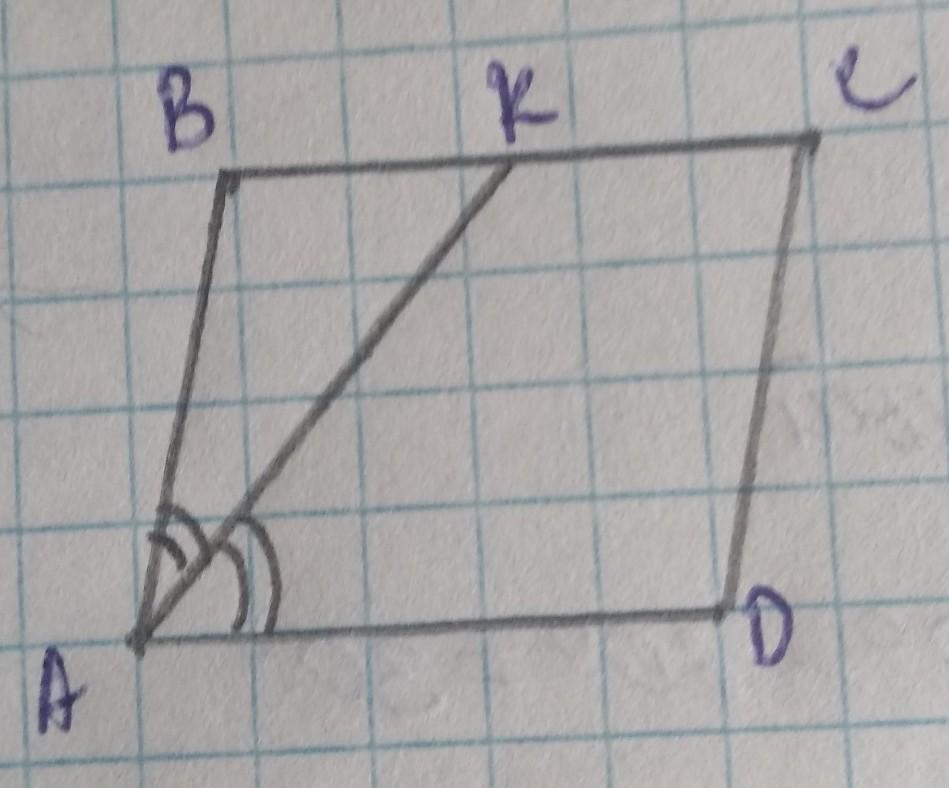
помогите пожалуйста. доказать что АВК - р/б.
геометрия*

Приложения:

Ответы

Автор ответа: Regent1828

Очень неудачный рисунок.

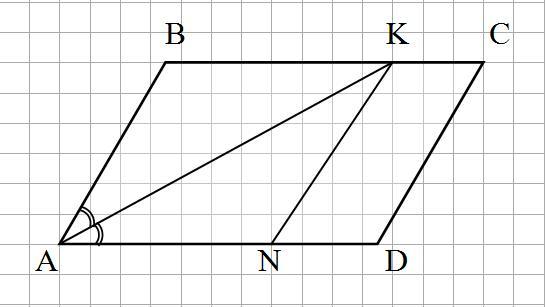
Достроим отрезок KN так, что KN || AB

Тогда в параллелограмме ABKN:

AK - диагональ и биссектриса угла А.

Собственно, этого уже достаточно. Так как параллелограммом, в котором диагональ является биссектрисой, может быть только ромб.

Следовательно АВ = ВК и треугольник АВК - равнобедренный.

Приложения:

Regent1828: У Вас вопрос по литературе. С чего Вы решили, что я смогу Вам помочь?

ParkKarina: Извините, но оказалось, что рисунок правильный, у него есть решение.

Regent1828: На Вашем рисунке визуально угол ВАК в 2 раза меньше угла KAD, а по условию они равны. Поэтому рисунок неудачный. Если не сказать, - неправильный.

ParkKarina: Наверное мне тогда нужно было уточнить, что АК - биссектриса.

Regent1828: Это и так понятно из равенства углов...))

Regent1828: Вследствие этого и треугольник, который Вы пытаетесь представить равнобедренным, никаким боком на равнобедренный не похож..))

ParkKarina: Вы дали мне мысль, дальше я сама, все равно спасибо. Вроде уже поняла, как дальше решать.

Regent1828: Можно через накрест лежащие углы доказать, но так длиннее. Рациональнее, все-таки, через ромб.

ParkKarina: Мы еще не проходили ромб)

Regent1828: У Вас нарисован параллелограмм. Ромб - частный случай параллелограмма...))

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Математика, автор: mamutovasabina124

{х+2у=5
{3х-2к=-17
20баллов