Предмет: Алгебра,
автор: Аноним
решить уравнение...........................................................................
Приложения:
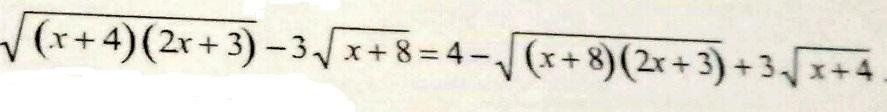
Аноним:
Тут решений нет?
x = 5
Ответы
Автор ответа:
3
Задание. Решить уравнение:
√((x+4)(2x+3)) - 3√(x+8) = 4 - √((x+8)(2x+3)) + 3√(x+4)
Решение:
Произведение равно нулю в том случае, когда хотя бы один из множителей обращается к нулю
Это уравнение решений не имеет, поскольку не выполняется одновременно и
(левая часть положительно)
Возводим обе части уравнения до квадрата
Снова возводим до квадрата обе части уравнения
Если подставить корень х = 1 в уравнение то равенство не выполняется, т.е. корень посторонний. Для корня х = 5 равенство верно.
Ответ: х = 5.
Похожие вопросы
Предмет: География,
автор: zuln31222
Предмет: Математика,
автор: Princess3729
Предмет: Английский язык,
автор: rustemhadiev9395
Предмет: Математика,
автор: Мнение
Предмет: Биология,
автор: nowichok