Question

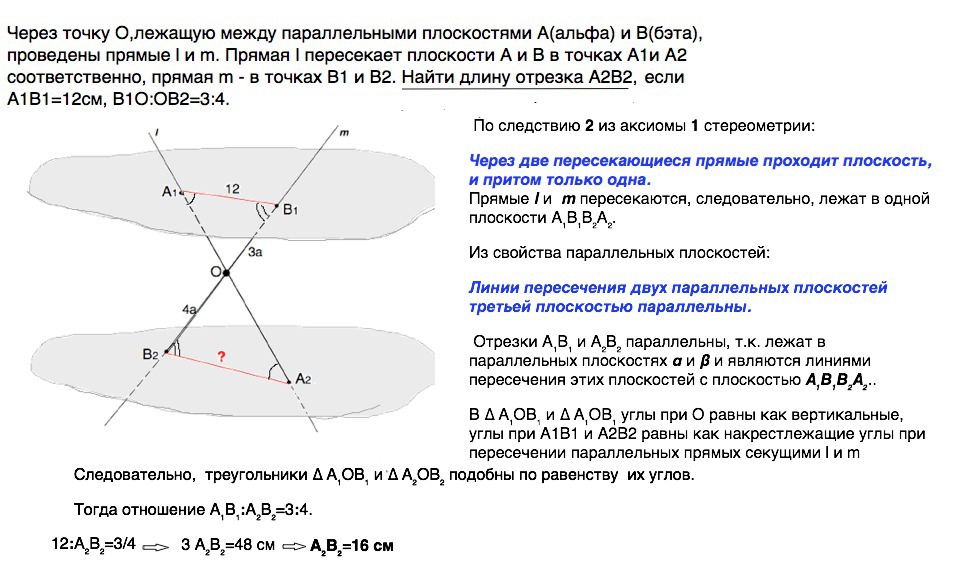
Через точку О,лежащую между параллельными плоскостями A(альфа) и В(бэта), проведены прямые l и m. Прямая l пересекает плоскости A и B в точках А1и А2 соответственно, прямая m - в точках В1 и В2. Найти длину отрезка А2В2,если А1В1=12см, В1О:ОВ2=3:4.

Answer 1

 По следствию 2 из аксиомы 1 стереометрии: 

Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Прямые l и  m пересекаются, следовательно, лежат в одной плоскости А₁В₁В₂А₂. 

Из свойства параллельных плоскостей: 

Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.

 Отрезки А₁В₁ и А₂В₂ параллельны, т.к. лежат в параллельных плоскостях α и β и являются линиями пересечения этих плоскостей с плоскостью А₁В₁В₂А₂..

В ∆ А₁ОВ₁ и ∆ А₁ОВ₁ углы при О равны как вертикальные, и углы при А₁В₁ и А₂В₂ равны как накрестлежащие  при пересечении параллельных прямых секущими l и m

Следовательно, 

треугольники ∆ А₁ОВ₁ и ∆ А₂ОВ₂ подобны по равенству углов. 

Тогда отношение А₁В₁: А₂В₂=3:4.

12:А₂В₂=3/4

3 А₂В₂=48 см

А₂В₂=16 см