Предмет: Математика,
автор: VAlDEROR
100 баллов! Решить уравнение и дать кратко объяснение решения.
25^|x+3| - 2*5^(|x+3|-1) - 3 = 0
То что в скобрах, значит всё в степени.
Ответы
Автор ответа:
63
Пусть и при этом
, получим
Корень , т.е. не удовлетворяет условию t > 0. Выполним обратную замену.
Автор ответа:
43
Ответ:
Пошаговое объяснение:
Приложения:
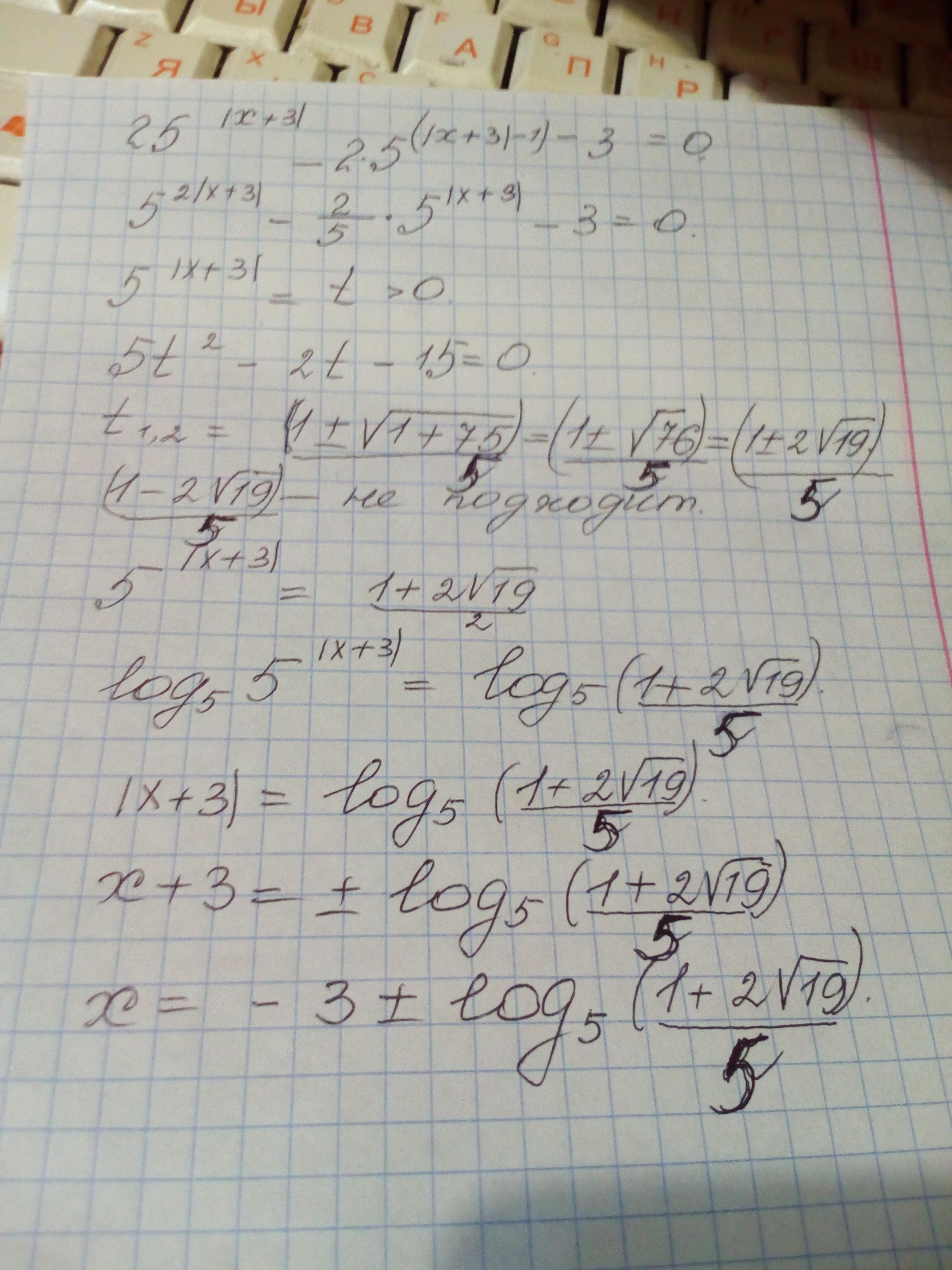
lugyar1997:
щеез
Похожие вопросы
Предмет: Алгебра,
автор: magat445
Предмет: Математика,
автор: azinovkin313s
Предмет: Литература,
автор: diaszeksenov6
Предмет: География,
автор: CmotrGo
Предмет: Математика,
автор: Мнение